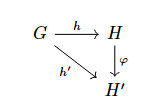本文原为泛代数学习笔记, 后来作为大三代数几何课程的期末论文上交.
泛代数基础
基础构造
定义(笛卡尔积)
设 $I$ 是指标集, 对于每个 $i \in I$, $A_i$ 是一个集合, 集合族 $\{A_i\}_{i \in I}$ 的笛卡尔积, $\prod_{i \in I} A_i$, 定义为
$$
\prod_{i \in I} A_i = \{f \mid f\colon I \to \bigcup_{i \in I} A_i, \forall i \in I, f(i) \in A_i\}.
$$
当 $I$ 为有限集时, 比如设 $|I|=n$, 等价的将 $\prod_{i \in I} A_i$ 中的元素记作 $n$ 元有序组 $(a_1,\cdots,a_n), a_i\in A_i$, 特别的, 当 $I$ 是空集时, 空积为一元集 $\{\emptyset\}$.
当 $A=A_i=A_j, i,j\in I$ 时, 笛卡尔积记作 $A^I$, 若 $|I|=n$, 也记作 $A^n$.
定义(二元关系)
设 $A$ 和 $B$ 是两个集合, 从 $A$ 到 $B$ 的二元关系 $\sim$ 是 $A \times B$ 的一个子集, 即 $\sim \subseteq A \times B$, 若 $(a,b)\in \sim$, 则称 $a$ 和 $b$ 有关系 $\sim$, 记作 $a\sim b$. 若 $A=B$, 则称 $\sim$ 是 $A$ 上的一个二元关系.
泛代数
定义(n元函数)
对于一个非空集合 $A$, $A$ 上的一个 $n$ 元函数或 $n$ 元运算是一个从 $A^n$ 到 $A$ 的函数, $n$ 是 $f$ 的元数, $(a_1, \ldots, a_n)$ 在 $n$ 元运算 $f$ 下的的像用 $f(a_1, \ldots, a_n)$ 表示. 如果 $A$ 上的运算 $f$ 的元数为零, 则称为零元运算, 它完全由 $A^0=\{\emptyset\}$ 中唯一元素 $\emptyset$ 在 $A$ 中的像 $f(\emptyset)$ 确定, 因此零元运算一般认为是 $A$ 中的一个元素.
我们这里只考虑有限元运算而不考虑无限元运算, 所以当我们说运算的时候默认是有限元运算.
一些特殊的函数在书写时按照通常的习惯书写, 例如二元函数加法 $+(a,b)$ 可写作 $a+b$, 一元函数取逆 $^{-1}(a)$ 可写作 $a^{-1}$, 零元函数单位元 $1(\emptyset)$ 则直接写作 $1$.
定义(型)
一个型或标签或语言, 是一个函数符号的集合 $\mathcal{F}$, 其中每个 $\mathcal{F}$ 的元素 $f$ 都关联一个非负整数 $n$, 称为 $f$ 的元数, 则 $f$ 称为一个 $n$ 元函数符号, $\mathcal{F}$ 中 $n$ 元函数符号组成的子集用 $\mathcal{F}_n$ 表示.
定义(代数)
如果 $\mathcal{F}$ 是一个型, 那么 $\mathcal{F}$ 型的代数 $\mathbf{A}$ 定义为一个有序对 $(A, F)$, 其中 $A$ 是一个非空集合, 称为 $\mathbf{A} = (A, F)$ 的论域或宇宙或全域, $F$ 称为 $A$ 上的函数集或运算集, 使得对于 $\mathcal{F}$ 中的每个 $n$ 元函数符号 $f$, 都存在一个 $A$ 上的 $n$ 元运算 $f^{\mathbf{A}}$, 在不引起歧义的情况下, 我们使用 $f$ 来表示 $f^{\mathbf{A}}$. 如果 $\mathcal{F}$ 是有限集, $\mathcal{F} = \{f_1, \cdots, f_k\}$, 我们通常用 $(A, f_1, \cdots, f_k)$ 来代替 $(A, F)$, 其中函数符号按元数降序排列.
约定代数一般使用粗体字母表示.
当论域 $A$ 为单元集时, 称 $\mathbf{A}$ 为平凡代数.
例(群)
一个群 $\mathbf{G}$ 是一个 $\{\cdot , {}^{-1}, 1\}$ 型代数 $(G,\cdot , {}^{-1}, 1)$, 其中 $\cdot$ 是二元运算, ${}^{-1}$ 是一元运算, $1$ 是零元运算, 并且要满足以下公式:
$\mathrm{(1)}$ $x \cdot (y \cdot z) \approx (x \cdot y) \cdot z;$
$\mathrm{(2)}$ $x \cdot 1 \approx 1 \cdot x \approx x ;$
$\mathrm{(3)}$ $x \cdot x^{-1} \approx x^{-1} \cdot x \approx 1.$
在一些抽象代数课本中通常不将取逆 $^{-1}$ 当作一个运算, 而是将上述定义中的第三条公式换成含量词的公理: 对任意的 $x\in G$, 存在元素 $y$ 使得 $x \cdot y \approx y \cdot x \approx 1$. 我们不采用这种定义方式, 因为如果这样定义, 在后续定义的子代数中, 群的子代数可能只是半群而不一定是群.
例(环)
环可以看作含两个二元运算, 加法和乘法, 一个一元运算, 加法逆元, 一个零元运算, 加法单位元 $0$, 的代数, 幺环则多一个零元运算, 即乘法单位元 $1$. 域则通常不能被看作代数, 因为域上的乘法逆只对非零元有定义, 即所谓的偏函数, 在泛代数中, 域只能看作特殊的环. 域也就是所谓的偏代数, 但我们在这里不考虑偏代数.
例($R$-模)
R-模即环 R 作用到交换群上得到的结构, 其上有无穷多个一元函数, 由左乘作用定义.
同态与同构
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F’)$ 是 $\mathcal{F}$ 型的两个代数, 则 $F$ 和 $F’$ 有一一对应 $f^{\mathbf{A}}\mapsto f^{\mathbf{B}}$.
定义(同态)
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是 $\mathcal{F}$ 型的两个代数, $\alpha$ 是 $A \to B$ 的映射, 如果对于每个 $n$ 元函数 $f \in \mathcal{F}$, 对于 $a_1, \cdots, a_n \in A$, 有
$$
\alpha (f^{\mathbf{A}}(a_1, \cdots, a_n)) = f^{\mathbf{B}}(\alpha (a_1), \cdots, \alpha (a_n)),
$$
则称 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的同态.
定义(同构)
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是同型的两个代数, 设 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的同态, 如果 $\alpha$ 是双射, 则称 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的同构, 记作 $\mathbf{A} \cong \mathbf{B}$, 称 $\mathbf{A}$ 与 $\mathbf{B}$ 同构.
同态为单射则称为单同态, 同态为满射则称为满同态, 从一个代数到自身的同态称为自同态, 从一个代数到自身的同构称为自同构.
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F’)$ 是 $\mathcal{F}$ 型的两个代数, 从 $\mathbf{A}$ 到 $\mathbf{B}$ 的所有同态记作 $\operatorname{Hom}(\mathbf{A},\mathbf{B})$.
容易验证, 同态的复合仍是同态, 若一对同态互逆, 则它们是同构.
定义(核)
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是同型的两个代数, 设 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的同态, 那么 $\alpha$ 的核, 记作 $\ker(\alpha)$, 定义为 $\mathbf{A}$ 上的一个二元关系
$$
\ker(\alpha) = \{(a, b) \in A^2 \mid \alpha(a) = \alpha(b)\}.
$$
子代数
定义(子代数)
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是 $\mathcal{F}$ 型的两个代数, 如果 $B \subseteq A$ 并且 $\mathbf{B}$ 中的每个运算都是 $\mathbf{A}$ 中相应运算的限制, 即如果 $f^{\mathbf{A}}$ 是 $\mathbf{A}$ 中的一个 $n$ 元运算, 并且 $a_1, \cdots, a_n \in B$, 那么 $f^{\mathbf{B}}(a_1, \ldots, a_n) \in B$, 则称 $B$ 是 $\mathbf{A}$ 的一个子论域, $\mathbf{B}$ 是 $\mathbf{A}$ 的一个子代数, 记作 $\mathbf{B} \le \mathbf{A}$.
定义(嵌入)
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是同型的两个代数, 设 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的同态, 如果 $\alpha$ 是单射, 则称 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的嵌入.
若 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的嵌入, 则 $\alpha(A)$ 是 $\mathbf{B}$ 的子论域, 若记 $\alpha(\mathbf{A})=(\alpha(A),F’)$, 则 $\alpha(\mathbf{A})$ 是 $\mathbf{B}$ 的子代数.
定义(生成)
给定一个代数 $\mathbf{A}=(A,F)$, 对于 $X \subseteq A$, 定义
$$
\operatorname{Sg}(X) = \bigcap \{B \mid X \subseteq B \text{ 且 } B \text{ 是 } \mathbf{A} \text{ 的一个子论域} \}.
$$
称 $\operatorname{Sg}(X)$ 为 $X$ 生成的子论域.
若 $\operatorname{Sg}(X)=A$, 则称 $X$ 生成 $\mathbf{A}$, 若 $X$ 还是有限集, 则称 $\mathbf{A}$ 是有限生成的.
积代数
定义(直积)
设 $I$ 是指标集, $\{\mathbf{A}_i=(A_i,F_i)\}_{i \in I}$ 是一族 $\mathcal{F}$ 型的代数, 它们的直积 $\mathbf{A} = \prod_{i \in I} \mathbf{A}_i$ 是一个代数, 其论域为 $\prod_{i \in I} A_i$, 并且对于 $n$ 元函数 $f \in \mathcal{F}$ 和 $a_1, \cdots, a_n \in \prod_{i \in I} A_i$, 有
$$
f^{\mathbf{A}}(a_1, \cdots, a_n)(i) = f^{\mathbf{A}_i}(a_1(i), \cdots, a_n(i)), i \in I.
$$
空积 $\prod_{i \in \emptyset} \mathbf{A}_i$ 是论域为 $\{\emptyset\}$ 的平凡代数.
定义(投影)
设 $I$ 是指标集, $\{\mathbf{A}_i=(A_i,F_i)\}_{i \in I}$ 是一族同型的代数, 它们的直积为 $\mathbf{A} = \prod_{i \in I} \mathbf{A}_i$, 定义投影映射为
$$
\begin{align*}
\pi_j \colon \prod_{i \in I} A_i &\to A_j\\
a &\mapsto a(j).
\end{align*}
$$
定理(直积的交换约束和结合约束)
如果 $\mathbf{A}_1$, $\mathbf{A}_2$, 和 $\mathbf{A}_3$ 是三个同型的代数, 那么有 $\mathbf{A}_1 \times \mathbf{A}_2 \cong \mathbf{A}_2 \times \mathbf{A}_1$, $\mathbf{A}_1 \times (\mathbf{A}_2 \times \mathbf{A}_3) \cong (\mathbf{A}_1 \times \mathbf{A}_2) \times \mathbf{A}_3$.
显然交换约束和结合约束可以推广到任意积, 此处省略.
定义(不可直积分解)
如果一个代数 $\mathbf{A}$ 不同构于两个非平凡代数的直积, 则称代数 $\mathbf{A}$ 是不可直积分解的.
同余与商代数
定义(等价关系集)
集合 $A$ 上所有等价关系组成的集合记作 $\operatorname{Eq}(A)$.
定义(同余关系)
设 $\mathbf{A}=(A,F)$ 是 $\mathcal{F}$ 型代数, $\equiv \in \operatorname{Eq}(A)$, 对于任意的 $a_1, \cdots, a_n , b_1 , \cdots , b_n \in A$ 和 $n$ 元函数 $f \in \mathcal{F}_n$, 当 $a_i\equiv b_i,1\le i\le n$ 时有
$$
f^{\mathbf{A}}(a_1,\cdots,a_n)\equiv f^{\mathbf{A}}(b_1,\cdots,b_n)
$$
成立, 则称 $\equiv$ 是 $\mathbf{A}$ 上的一个同余关系.
$\mathbf{A}$ 上的所有同余关系组成的集合记作 $\operatorname{Con}(\mathbf{A})$.
定理(同余的任意交仍是同余)
设 $S$ 是代数 $\mathbf{A}$ 上的任意一族同余关系, 即 $S\subseteq\operatorname{Con}(\mathbf{A})$, 则 $\cap S$ 仍是同余.
定义(生成同余)
设 $\mathbf{A}=(A,F)$ 是一个代数, $R\subseteq A\times A$, 则由 $R$ 生成的同余为包含 $R$ 的最小同余关系, 记作 $\operatorname{Cg}^{\mathbf{A}}(R)$, 即 $\operatorname{Cg}^{\mathbf{A}}(R)=\cap\{\equiv\in\operatorname{Con}(\mathbf{A})\mid R\subseteq\equiv\}$.
若 $R$ 是有限集, 则称同余 $\operatorname{Cg}^{\mathbf{A}}(R)$ 是有限生成的, 若 $R$ 形如 $\{(x_1,x_2)\}$, 则称 $\operatorname{Cg}^{\mathbf{A}}(R)=\operatorname{Cg}^{\mathbf{A}}(x_1,x_2)$ 是一个主同余.
显然主同余在环论中对应环的主理想, 例如整数环中 $\operatorname{Cg}^{\mathbf{A}}(3,5)$ 即为主理想 $(2)$.
定理(生成同余的构造)
设 $\mathbf{A}=(A,F)$ 是一个 $\mathcal{F}$ 型代数, $R\subseteq A\times A$, 先由 $R$ 定义集合 $R_1$,
$$
R_1=R\cup\{(a,a)\mid a\in A\}\cup\{(a,b)\mid (b,a)\in R,a,b\in A)\},
$$
再递归的定义集合 $R_n$,
$$
\begin{align*}
R_n=&\{(a,c)\mid (a,b)\in R_{n-1},(b,c)\in R_{n-1},a,b,c\in A\}\cup\\
&\{(f^{\mathbf{A}}(a_1,\cdots,a_n),f^{\mathbf{A}}(b_1,\cdots,b_n))\mid f\in \mathcal{F}_n,(a_i,b_i)\in R_{n-1},a_i,b_i\in A,1\le i\le n\},
\end{align*}
$$
则
$$
\operatorname{Cg}^{\mathbf{A}}(R)=\bigcup_{n=1}^\infty R_n.
$$
定义(诺特代数)
如果代数 $\mathbf{A}$ 的任意同余都可以由一个有限集生成, 则称 $\mathbf{A}$ 是一个诺特代数.
使用与环论中相同的方法可以证明, 代数 $\mathbf{A}$ 是诺特代数当且仅当 $\operatorname{Con}(\mathbf{A})$ 中不存在无限长的严格同余升链.
定理
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是同型的两个代数, 设 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的同态, 那么 $\alpha$ 的核 $\ker(\alpha)$, 是 $\mathbf{A}$ 上的一个同余关系.
定义(商代数)
设 $\mathbf{A}=(A,F)$ 是 $\mathcal{F}$ 型代数, 若 $\equiv$ 是 $\mathbf{A}$ 上的一个同余关系, 则 $\mathbf{A}$ 商掉 $\equiv$ 得到的商代数记作 $\mathbf{A}/\equiv$, 它的论域为商集 $A/\equiv$, 其中的元素记作 $[a]_{\equiv}$, 其中 $a\in A$ 是等价类的代表元, $\mathbf{A}/\equiv$ 上的函数由
$$
f^{\mathbf{A}/\equiv}([a_1]_{\equiv},\cdots,[a_n]_{\equiv})=[f^{\mathbf{A}}(a_1,\cdots,a_n)]_{\equiv}
$$
定义, 其中 $f\in\mathcal{F}$ 为 $n$ 元函数符号, $a_1,\cdots,a_n\in A$.
在无歧义的情况下, $[a]_{\equiv}$ 简写为 $[a]$.
设 $\mathbf{G}$ 是一个群, $\equiv$ 是其上的一个同余关系, 则 $[1]$ 便是一个正规子群, 反之, 若 $\mathbf{N}$ 是 $\mathbf{G}$ 的一个正规自群, 则由
\[a\equiv b\Longleftrightarrow a\cdot b^{-1}\in N\]
定义的二元关系便是一个同余关系, 且显然有 $[1]=N$. 同理, 环中的 $[0]$ 便对应理想.
定义(自然同态)
设 $\mathbf{A}=(A,F)$ 是一个代数, 若 $\equiv$ 是 $\mathbf{A}$ 上的一个同余关系, 则从 $\mathbf{A}$ 到商代数 $\mathbf{A}/\equiv$ 有一个自然满同态, 由下式定义,
$$
\begin{align*}
\pi \colon A &\to A/\equiv\\
a &\mapsto [a].
\end{align*}
$$
同态基本定理
定理(第一同构定理)
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是同型的两个代数, 设 $\alpha$ 是 $\mathbf{A}$ 到 $\mathbf{B}$ 的同态, 则 $\mathbf{A}/\ker(\alpha)\cong \alpha(\mathbf{A})$.
证明
设 $A \to A/\ker(\alpha)$ 的自然同态为 $\pi$, 设映射 $\beta\colon A/\ker(\alpha)\to \alpha(A)$ 由 $\alpha=\beta\circ\pi$ 确定, 则 $\beta$ 即为所求的同构映射.
定义
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是同型的两个代数, $\mathbf{B}$ 是 $\mathbf{A}$ 的子代数, $\equiv$ 是 $\mathbf{A}$ 上的一个同余关系, 令
$$
\equiv\mid_B = \equiv \cap (B \times B),
$$
称为 $\equiv$ 在 $B$ 上的的限制, 并令
$$
B^\equiv = \{a \in A \mid [a] \cap B \ne \emptyset \},
$$
设 $\mathbf{B}^\equiv$ 为 $B^\equiv$ 生成的 $\mathbf{A}$ 的子代数.
定理(第二同构定理)
设 $\mathbf{A}=(A,F)$ 和 $\mathbf{B}=(B,F')$ 是同型的两个代数, $\mathbf{B}$ 是 $\mathbf{A}$ 的子代数, $\equiv$ 是 $\mathbf{A}$ 上的一个同余关系, 则 $\equiv\mid_B$ 是 $\mathbf{B}$ 上的同余关系, $\equiv\mid_{B^\equiv}$ 是 $\mathbf{B^\equiv}$ 上的同余关系, 且
$ \mathbf{B}/\equiv\mid_B\cong\mathbf{B}^\equiv/\equiv\mid_{B^\equiv}$.
证明
同构由 $[b]_{\equiv\mid_B}\mapsto[b]_{\equiv\mid_{B^{\equiv}}}$ 给出.
定义
设 $\mathbf{A}=(A,F)$ 是一个代数, 若 $\equiv_1,\equiv_2\in \operatorname{Con}(\mathbf{A})$, 且 $\equiv_1\subseteq\equiv_2$, 定义
$$
\equiv_2/\equiv_1=\{([a]_{\equiv_1},[b]_{\equiv_1})\in (A/\equiv_1)^2 \mid (a,b)\in\equiv_2\}.
$$
定理(第三同构定理)
设 $\mathbf{A}=(A,F)$ 是一个代数, 若 $\equiv_1,\equiv_2\in \operatorname{Con}(\mathbf{A})$, 且 $\equiv_1\subseteq\equiv_2$, 则 $\equiv_2/\equiv_1$ 是 $\mathbf{A}/\equiv_1$ 上的同余关系, 且 $(\mathbf{A}/\equiv_1)/(\equiv_2/\equiv_1)\cong \mathbf{A}/\equiv_2$.
证明
同构由 $[[a]_{\equiv_1}]_{\equiv_2/\equiv_1}\mapsto[a]_{\equiv_2}$ 给出.
设 $\mathbf{A}=(A,F)$ 是一个代数, 显然 $\operatorname{Con}(\mathbf{A})$ 在集合的包含关系下构成一个偏序集, 并且这个偏序集中有最小元和最大元, 最小元即为 $A\times A$ 的对角线集
\[\Delta_A=\{(a,a)\mid a\in A\},\]
最大元即为 $A\times A$ 本身, 我们对偶的将它记作 $\nabla_A=A\times A$.
定义(平凡同余和真同余)
代数 $\mathbf{A}=(A,F)$ 中的同余 $\Delta_A=\{(a,a)\mid a\in A\}$ 和 $\nabla_A=A\times A$ 称为 $\mathbf{A}$ 的平凡同余, 除此之外的同余称为真同余.
定义(偏序集的闭区间)
设 $(P,\le)$ 是偏序集, 设 $a, b \in X$, 则闭区间 $[a,b]$ 定义为
$$
[a, b] = \{ x \in P \mid a \leq x \leq b \}.
$$
显然偏序集的闭区间是子偏序集, 下面叙述泛代数的对应定理, 有时也称为第四同构定理.
定理(对应定理)
设 $\mathbf{A}=(A,F)$ 是一个代数, $\equiv\in\operatorname{Con}(\mathbf{A})$, 则 $[\equiv,\nabla_A]\cong \operatorname{Con}(\mathbf{A}/\equiv)$ 是序同构.
证明
序同构由 $\equiv'\mapsto\equiv'/\equiv$ 给出.
定义(单代数)
设 $\mathbf{A}$ 是一个代数, 若 $\operatorname{Con}(\mathbf{A})=\{\Delta_A,\nabla_A\}$, 则称 $\mathbf{A}$ 是单代数, 若 $\mathbf{A}$ 的论域是有限集, 则称 $\mathbf{A}$ 为有限单代数.
定义(极大同余)
设 $\mathbf{A}$ 是一个代数, $\equiv\in\operatorname{Con}(\mathbf{A})$ 且 $\equiv\neq\nabla_A$, 若 $[\equiv,\nabla_A]=\{\equiv,\nabla_A\}$, 则称 $\equiv$ 是 $\mathbf{A}$ 的极大同余.
定理
设 $\mathbf{A}$ 是一个代数, $\equiv\in\operatorname{Con}(\mathbf{A})$, $\mathbf{A}/\equiv$ 是一个单代数当且仅当 $\equiv$ 是极大同余.
证明
由对应定理显然.
HSP定理
本章内容并未完全忠实于参考文献, 但此处定义和定理与参考文献里的是等价的.
项代数
定义(项)
设 $X$ 是一个集合, 其中元素称为变元, 设 $\mathcal{F}$ 为一个型, 定义基于 $X$ 的 $\mathcal{F}$ 型项的集合 $T(X)$ 是满足以下条件的最小集合:
$\mathrm{(1)}$ $X \cup \mathcal{F}_0 \subseteq T(X)$;
$\mathrm{(2)}$ 若 $p_1,\cdots,p_n \in T(X)$ 且 $f \in \mathcal{F}_n$, 则 $f(p_1, \dots, p_n) \in T(X)$.
$T(X)$ 中元素称为项.
对于一个项 $p$, 易知 $p$ 中含有的变元只有有限个, 比如 $p$ 含有的变元在 $x_1,\cdots,x_n$ 之中, 那么可将 $p$ 记作 $p(x_1,\cdots,x_n)$.
定义(项代数)
给定型 $\mathcal{F}$ 和集合 $X$, 项的集合为 $T(X) \neq \emptyset$, 则 $X$ 上的 $\mathcal{F}$ 型项代数记作 $\mathbf{T}(X)$, 其论域为集合 $T(X)$, 其上运算满足
$$
\begin{align*}
f^{\mathbf{T}(X)} \colon T(X)^n &\to T(X)\\
(p_1, \dots, p_n) &\mapsto f(p_1, \dots, p_n),
\end{align*}
$$
其中 $f \in \mathcal{F}_n$, $p_i \in T(X)$, $1 \leq i \leq n$. 亦称 $\mathbf{T}(X)$ 为 $X$ 生成的项代数.
项代数也称为绝对自由代数.
定义(项函数)
对于集合 $X$ 上 $\mathcal{F}$ 型的项 $p(x_1, \cdots, x_n)$ 和一个 $\mathcal{F}$ 型的代数 $\mathbf{A}$, 我们递归的定义一个映射 $p^{\mathbf{A}}: A^n \rightarrow A$ 如下:
$\mathrm{(1)}$ 如果 $p$ 是一个变元 $x_i$, 那么
$$
p^{\mathbf{A}}(a_1, \cdots, a_n) = a_i,
$$
其中 $a_1, \dots, a_n \in A$;
$\mathrm{(2)}$ 如果 $p$ 的形式是 $f(p_1(x_1, \cdots, x_n), \cdots, p_k(x_1, \cdots, x_n))$, 其中 $f \in \mathcal{F}_k, p_i\in T(X),x_j\in X$, 那么
$$
p^{\mathbf{A}}(a_1, \cdots, a_n) = f^{\mathbf{A}}(p_1^{\mathbf{A}}(a_1, \cdots, a_n), \cdots, p_k^{\mathbf{A}}(a_1, \cdots, a_n)).
$$
称 $p^{\mathbf{A}}$ 是对应于项 $p$ 在 $\mathbf{A}$ 上的项函数.
簇
定义(等式)
给定型 $\mathcal{F}$ 和集合 $X$, 项的集合为 $T(X) \neq \emptyset$, 则 $X$ 上的 $\mathcal{F}$ 型等式形如
$$
p\approx q,
$$
其中 $p,q\in T(X)$, 记 $X$ 上所有 $\mathcal{F}$ 型等式组成的集合为 $\operatorname{Id}_{\mathcal{F}}(X)$, 它与 $T(X)\times T(X)$ 之间有自然的双射, 于是等式可以理解为 $T(X)$ 上的二元关系.
$\operatorname{Id}_{\mathcal{F}}(X)$ 的子集称为等式集或理论, 通常用 $\Sigma$ 表示, 即 $\Sigma\subseteq\operatorname{Id}_{\mathcal{F}}(X). $
定义(满足)
给定型 $\mathcal{F}$ 和集合 $X$, 项的集合为 $T(X)$, 设 $\mathbf{A}=(A,F)$ 是一个 $\mathcal{F}$ 型代数, 若对于两个项 $p(x_1,\cdots,x_n),q(x_1,\cdots,x_n)\in T(X)$, 有
$$
p^{\mathbf{A}}(a_1,\cdots,a_n)=q^{\mathbf{A}}(a_1,\cdots,a_n),\forall a_1,\cdots, a_n\in A,
$$
则称代数 $\mathbf{A}$ 满足 $p\approx q$ 或 $\mathbf{A}$ 是 $p\approx q$ 的一个模型, 记作 $\mathbf{A}\models p\approx q$.
若 $\Sigma$ 是公式集, 且 $\mathbf{A}$ 满足 $\Sigma$ 中的每一条等式, 则称 $\mathbf{A}$ 满足 $\Sigma$ 或 $\mathbf{A}$ 是 $\Sigma$ 的一个模型, 记作 $\mathbf{A}\models \Sigma$.
约定使用无衬线字体表示范畴, 多数泛代数教材中使用了类的概念, 但为避免集合论的麻烦, 这里使用范畴语言叙述.
定义(簇)
给定型 $\mathcal{F}$, 集合 $X$ 及其上等式集 $\Sigma$, 一个簇是一个范畴 $\mathsf{V}$, 其对象为 $\Sigma$ 的全体 $\mathcal{F}$ 型模型, 态射为代数间同态, 这个簇记作 $\mathsf{V}=\operatorname{Mod}(\Sigma)$.
例
群范畴 $\mathsf{Grp}$ 是一个簇, 环范畴 $\mathsf{Rng}$ 是一个簇, 幺环范畴 $\mathsf{Ring}$ 是一个簇, 交换幺环范畴 $\mathsf{CRing}$ 是一个簇, 交换幺环 $R$ 上的模范畴 $R-\mathsf{Mod}$ 是一个簇.
定义(演绎闭包)
设 $\mathsf{A}$ 是由一些 $\mathcal{F}$ 型代数及其同态组成的范畴, 记 $\operatorname{Id}(\mathsf{A})$ 是 $\mathsf{A}$ 满足的 $X$ 上所有 $\mathcal{F}$ 型等式组成的等式集, 则对于等式集 $\Sigma$, 称 $\operatorname{Id}(\operatorname{Mod}(\Sigma))$ 为 $\Sigma$ 的演绎闭包. 若 $\Sigma=\operatorname{Id}(\operatorname{Mod}(\Sigma))$, 则称 $\Sigma$ 是演绎闭的.
显然 $\Sigma\subseteq \operatorname{Id}(\operatorname{Mod}(\Sigma))$, 且 $\operatorname{Id}(\operatorname{Mod}(\operatorname{Id}(\operatorname{Mod}(\Sigma))))=\operatorname{Id}(\operatorname{Mod}(\Sigma))$, 这就是演绎闭包名称的来源.
可以证明, $\operatorname{Id}(\mathsf{A})$ 一定是演绎闭的. 若 $\Sigma$ 是演绎闭的, 则存在一个簇 $\mathsf{V}$ 满足 $\Sigma=\operatorname{Id}(\mathsf{V)}$.
称 $\operatorname{Mod}(\operatorname{Id}(\mathsf{A}))$ 为 $\mathsf{A}$ 生成的簇, 若 $\mathsf{A}$ 是单元集 ${\mathbf{A}}$, 则记作 $\operatorname{Mod}(\operatorname{Id}(\mathbf{A}))$, 显然 $\operatorname{Mod}(\operatorname{Id}(\cdot))$ 也是一个闭包算子, 称为同语闭包. 若范畴 $\mathsf{V}$ 是簇, 则 $\operatorname{Mod}(\operatorname{Id}(\mathsf{V}))=\mathsf{V}$, 即同语闭, 反之, 若一个代数范畴同语闭则一定是簇, 显然此时 $\Sigma=\operatorname{Id}(\mathsf{V})$.
设 $\mathsf{C}$ 是一个范畴, 其中对象为 $\mathcal{F}$ 型代数的范畴 $\mathsf{A}$, 态射为各对象自身的对象集 $\operatorname{Ob}(\mathsf{A})$ 之间的包含映射给出的范畴间的函子. 再设 $\mathsf{E}=\mathscr{P}(\operatorname{Id}{\mathcal{F}}(X))$ 为 $\operatorname{Id}{\mathcal{F}}(X)$ 的幂集, 它关于集合间包含关系构成一个偏序集, 可以将其做成一个范畴, 对象为所有等式集, 态射为包含映射. 这样, $\operatorname{Id}(\cdot)$ 和 $\operatorname{Mod}(\cdot)$ 即为 $\mathsf{C}$ 和 $\mathsf{E}$ 之间的一对伴随函子. 设 $\mathsf{V}$ 是所有簇组成的范畴, 它是 $\mathsf{C}$ 的子范畴, 设 $\mathsf{D}$ 是所有演绎闭的等式集组成的范畴, 它是 $\mathsf{E}$ 的子范畴, 则 $\operatorname{Id}(\cdot)$ 和 $\operatorname{Mod}(\cdot)$ 为 $\mathsf{V}$ 和 $\mathsf{D}$ 之间的范畴同构.
例
如果取簇为半群范畴 $\mathsf{Sg}$, 取 $X=\{a,b,c\}$, 若取 $\Sigma=\{(a\cdot b)\cdot c\approx a\cdot(b\cdot c)\}$, 则 $\operatorname{Mod}(\Sigma)=\mathsf{Sg}$, 但 $\operatorname{Id}(\operatorname{Mod}(\Sigma))=\operatorname{Id}(\mathsf{Sg})=\{(a\cdot a)\cdot a\approx a\cdot(a\cdot a),\cdots,(c\cdot c)\cdot c\approx c\cdot(c\cdot c)\}$, 这个集合中一共有 $3^3=9$ 个元素.
自由代数
定义(自由代数)
给定型 $\mathcal{F}$ 和集合 $X$, 对应的项代数为 $\mathbf{T}(X)$, $\Sigma$ 是一个等式集, 在 $\mathbf{T}(X)$ 上定义同余关系 $\sim$, 若 $p,q\in T(X)$, 则 $p\sim q \Longleftrightarrow p\approx q\in \operatorname{Id}(\operatorname{Mod}(\Sigma))$, 则商代数 $\mathbf{T}(X)/\sim$ 称为 $X$ 上的 $\mathcal{F}$ 型 $\Sigma$ 自由代数, 记作 $\mathbf{F}_{\Sigma}(X)$, 其论域记作 $F_{\Sigma}(X)$.
自由代数常简写为 $\mathbf{F}(X)$, 论域简写为 $F(X)$.
例
在所有岩浆组成的簇中, 自由代数与项代数是相同的, 因为岩浆满足的等式集为空集. 在自由岩浆中 $(a\cdot a)\cdot a$ 和 $a\cdot(a\cdot a)$ 是两个不同的元素.
定理(自由代数的泛性质)
给定型 $\mathcal{F}$, 集合 $X$ 及其上等式集 $\Sigma$, 设 $X$ 上的 $\mathcal{F}$ 型 $\Sigma$ 自由代数为 $\mathbf{F}_{\Sigma}(X)$, $\iota\colon X\to F_{\Sigma}(X)$ 是自然的映射, 则对 $\Sigma$ 的任意一个 $\mathcal{F}$ 型模型 $\mathbf{A}=(A,F)$ 和映射 $\iota'\colon X \to A$, 都存在一个唯一的同态 $\varphi\colon F_{\Sigma}(X)\to A$, 使得下图交换:
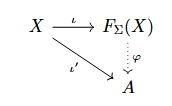
也有人直接使用泛性质定义自由代数, 即自由代数 $F_\Sigma(X)$ 是范畴 $\mathsf{M}(\Sigma)$ 中 $X$ 上的自由对象, 亦即自由函子 $U\colon\mathsf{Set}\to\mathsf{M}(\Sigma)$ 在 $X$ 处的像 $U(X)$, 自由函子与遗忘函子互相伴随, 此处不多赘述.
HSP定理
一些同型代数连同代数间同态组成的范畴 $\mathsf{C}$ 在取同态像, 取子代数, 取积代数下封闭的意思是, 对任意一个代数 $\mathbf{A}\in\operatorname{Ob}(\mathsf{C})$ 和从 $A$ 射出的同态 $\alpha$, 其同态像 $\alpha(\mathbf{A})\in\operatorname{Ob}(\mathsf{C})$, $\mathbf{A}$ 的任意子代数也在 $\operatorname{Ob}(\mathsf{C})$ 中, 对任意一族代数 ${\mathbf{A}i}{i\in I}\subseteq\operatorname{Ob}(\mathsf{C})$, 其中 $I$ 是指标集, 则积代数 $\prod_{i \in I} \mathbf{A}_i\in\operatorname{Ob}(\mathsf{C})$.
定义如下闭包算子 $H(\mathsf{C}), S(\mathsf{C}), P(\mathsf{C})$ 分别为:
$H(\mathsf{C})$ 为包含 $\mathsf{C}$ 的最小范畴, 使得 $\mathsf{C}$ 中代数的任意同态像都在 $H(\mathsf{C})$ 中;
$S(\mathsf{C})$ 为包含 $\mathsf{C}$ 的最小范畴, 使得 $\mathsf{C}$ 中代数的任意子代数都在 $S(\mathsf{C})$ 中;
$P(\mathsf{C})$ 为包含 $\mathsf{C}$ 的最小范畴, 使得 $\mathsf{C}$ 中代数的任意积代数都在 $P(\mathsf{C})$ 中.
若算子 $O_1$ 和 $O_2$ 是以上任意算子或其复合, 则 $O_1\le O_2$ 意味着 $O_1(\mathsf{C})\subseteq O_2(\mathsf{C})$, 并且算子的复合通常省略括号或复合符号.
定理
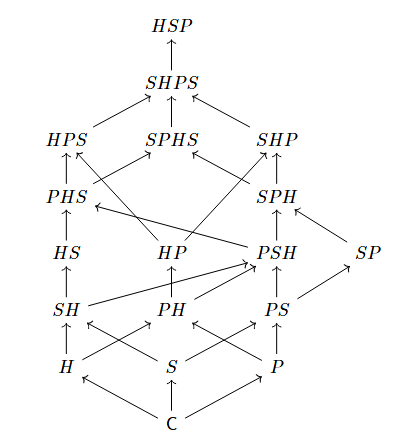
$SH\le HS$, $PS\le SP$, $PH\le HP$.
关于这三种闭包算子之间的强度关系, 有如下图表:
如图, $HSP$ 位于该图的最顶端, 实际上, 有以下定理.
定理
对于一个由一些同型代数连同代数间同态组成的范畴 $\mathsf{C}$, 包含它的最小的在取同态像, 取子代数, 取积代数下封闭的范畴正是 $H(S(P(\mathsf{C})))$.
定理
$\operatorname{Id}(\mathsf{C})=\operatorname{Id}(H(\mathsf{C}))=\operatorname{Id}(S(\mathsf{C}))=\operatorname{Id}(P(\mathsf{C}))=\operatorname{Id}(HSP(\mathsf{C}))$.
定理
给定型 $\mathcal{F}$ 和集合 $X$, $\Sigma$ 是一个等式集, $X$ 上的 $\mathcal{F}$ 型 $\Sigma$ 自由代数为 $\mathbf{F}_{\Sigma}(X)$, 则有
$$
\operatorname{Id}(\operatorname{Mod}(\Sigma))=\operatorname{Id}(\mathbf{F}_{\Sigma}(X)).
$$
定理
若一个由一些同型代数连同代数间同态组成的范畴 $\mathsf{C}$ 在取同态像, 取子代数, 取积代数下封闭, 即 $\mathsf{C}=HSP(\mathsf{C})$, 则有 $\mathsf{C}=\operatorname{Mod}(\operatorname{Id}(\mathsf{C))}$.
定理(HSP定理)
一些同型的代数连同代数间同态组成的范畴 $\mathsf{C}$ 是簇当且仅当它在取同态像, 取子代数, 取积代数下封闭.
HSP定理中的 H 指同态像 Homomorphic image, S 指子代数 Subalgebra, P 指积代数 Product.
HSP定理的证明
若 $\mathsf{V}$ 是簇, 设 $\mathsf{V}=\operatorname{Mod}(\Sigma)$, 因为 $\operatorname{Id}(\mathsf{V})=\operatorname{Id}(\operatorname{Mod}(\Sigma))=\operatorname{Id}(HSP(\mathsf{V}))$, 则 $HSP(\mathsf{V})\subseteq \operatorname{Mod}(\Sigma)=\mathsf{V}$, 而由因 $\mathsf{V}\subseteq HSP(\mathsf{V})$ 知 $\mathsf{V}=HSP(\mathsf{V})$, 即它在取同态像, 取子代数, 取积代数下封闭.
若一个由一些同型代数连同代数间同态组成的范畴 $\mathsf{C}$ 在取同态像, 取子代数, 取积代数下封闭, 即 $\mathsf{C}=HSP(\mathsf{C})$, 则有 $\mathsf{C}=\operatorname{Mod}(\operatorname{Id}(\mathsf{C))}$, 所以 $\mathsf{C}$ 是簇.
泛代数几何
在以下内容中, 可能会出现一些术语滥用现象, 为避免麻烦, 我们进行如下约定: 约定下文中提到的所有环均为交换幺环, 对于固定的环$R$, $R$-代数意指环$R$作用到环上得到的结构, 即使是在不会引起混淆的情况下也不能省略$R$前缀, 而单纯的代数则仍指上文提到的有序对$(A,F)$. 在古典代数几何中, 代数簇这个基本概念常被简称为簇, 但本文不使用这种简称, 文中提到的所有簇都为之前定义的特定代数组成的范畴.
本章的符号不沿用参考文献中的符号, 而是使用GTM52中的符号, 以着重体现泛代数几何是古典代数几何的推广这一事实.
泛代数观点下的古典代数几何
之前已经提到, 在泛代数的观点下, 域并不是一个代数, 而只能看做特殊的交换幺环.
定理
对于固定的交换幺环 $R$, 给定变量集 $X$, 以 $X$ 为变量 $R$ 上的多项式代数 $R[X]$ 定义为 $R$-交换代数范畴 $R$-$\mathsf{CAlg}$ 中的自由对象, 它同构于交换幺环范畴 $\mathsf{CRing}$ 中环 $R$ 与 $X$ 上的自由对象 $F(X)$ 的余积 $R\coprod F(X)$.
证明
由自由对象的泛性质, 对任意交换环 $S$ 和映射 $g\colon X\to S$, 存在唯一的态射 $\varphi$ 使下图交换,
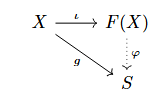
由余积的泛性质, 对于环 $S$ 和环同态 $\varphi\colon F(X)\to S$, 有唯一的环同态 $\psi$ 使下图交换,
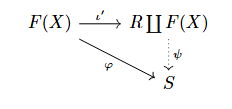
将两图连接即得交换图
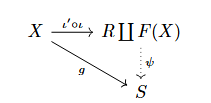
若 $S$ 同时为 $R$-代数, 该图依然成立, 便知 $R\coprod F(X)$ 为 $R$-$\mathsf{CAlg}$ 中的自由对象, 由自由对象唯一性知 $R\coprod F(X)$ 与 $R[X]$ 同构.
设 $k$ 是一个代数闭域, 给定有限变量集 $X$, 则 $k$ 上的多项式代数便是范畴 $k$-$\mathsf{CAlg}$ 中的自由对象, 即簇 $k$-$\mathsf{CAlg}$ 中的自由代数. 仿射空间定义为从 $X$ 到 $k$ 的所有映射组成的集合 $k^X$, 若 $\lvert X
vert=n$, 则记作 $k^n$.
任意一个集合间映射 $\mu\colon X\to k$ 都给出一个 $k$-代数间同态, 即代入映射 $\mu’\colon k[X]\to k$, 而每一个 $k$-代数间同态 $\mu’\colon k[X]\to k$ 都由 $x\mapsto\mu’(x),x\in X$ 给出一个集合间映射 $\mu\colon X\to k$, 若 $X={x_1,\cdots,x_n}$, $\mu$ 便对应 $k^{\lvert X
vert}$ 中的点 $(\mu’(x_1),\cdots,\mu’(x_n))$. 因此, 在泛代数几何中, 仿射空间定义为 $\operatorname{Hom}_{k\text{-}\mathsf{CAlg}}(k[X],k)$, 若 $\lvert X
vert=n$ 则称其为 $n$ 维仿射空间. 我们仍称仿射空间中的元素 $\mu$ 为点, 这种做法在很多时候是方便的.
对于一个多项式 $f\in k[X]$ 和仿射空间中的一个点 $\mu\in\operatorname{Hom}{k\text{-}\mathsf{CAlg}}(k[X],k)$, 若 $\mu(f)=0$, 则称 $f$ 在点 $\mu$ 处消失, 称 $\mu$ 是多项式 $f$ 的零点或根. 在点 $\mu$ 处消失的所有多项式组成的集合记作 $\ker\mu=\mu^{-1}(0)$, $f\in\ker\mu$ 等价于说 $\mu(f)=0$, 而多项式 $f$ 的全体零点组成的集合则为 ${\mu\in\operatorname{Hom}{k\text{-}\mathsf{CAlg}}(k[X],k]\mid \mu(f)=0}$.
对于多项式代数的任何一个子集 $T\subseteq k[X]$, 定义
\[Z(T)=\{\mu\in\operatorname{Hom}_{k\text{-}\mathsf{CAlg}}(k[X],k)\mid T\subseteq\mu^{-1}(0)\},\]
称为 $T$ 的零点集, 即使得 $T$ 中每个多项式都消失的点. 对于仿射空间的子集 $Y$, 定义
\[I(Y)=\bigcap_{\mu\in Y}\ker\mu,\]
称为 $Y$ 的理想. $Z(\cdot)$ 和 $T(\cdot)$ 给出仿射空间的幂集与多项式代数的幂集之间的一对伽罗瓦连接, 对于仿射空间的子集 $Y$, 如果存在多项式代数的子集 $T$ 使得 $Y=Z(T)$, 则称其为代数集, 对于多项式代数的子集 $T$, 如果存在仿射空间的子集 $Y$ 使得 $T=I(Y)$, 则称其为根理想, 这是因为由希尔伯特零点定理, 此时必有 $T=\sqrt{T}$.
至此, 古典代数几何中的一些基本定义已翻译成了泛代数的语言, 下一节中则直接在泛代数上定义这些概念.
基础构造
带常数的簇
本节做一些准备工作, 前文中已经看到了域在泛代数理论中的特殊性, 我们利用带常数的簇的概念处理这一特殊性, 其核心是把一个固定的代数当作该代数上的簇中的常数, 类似 $k$-模, $k$-代数.
设 $\mathsf{V}$ 是一个簇, $\mathbf{G}=(G,F)$ 是簇 $\mathsf{V}$ 中的一个对象, 构造一个新簇 $\mathsf{V}(\mathbf{G})$, 其中对象是簇 $\mathsf{V}$ 中存在满足如下条件的代数 $\mathbf{H}=(H,F’)$: 若存在从 $\mathbf{G}$ 到 $\mathbf{H}$ 的同态 $h$, 则 $\mathbf{H}$ 是 $\mathsf{V}(\mathbf{G})$ 中的对象, 称 $\mathbf{H}$ 为 $\mathbf{G}$ 上的代数, 强调同态 $h$ 时常将 $\mathbf{H}$ 写作 $(\mathbf{H},h)$. $\mathsf{V}(\mathbf{G})$ 中两个对象 $(\mathbf{H},h)$ 和 $(\mathbf{H}’,h’)$ 间的态射是使如下图交换的同态 $\varphi$,
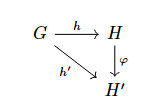
故 $\operatorname{Hom}{\mathsf{V}(\mathbf{G})}(\mathbf{H},\mathbf{H}’)$ 是 $\operatorname{Hom}\mathsf{V}(\mathbf{H},\mathbf{H}’)$ 的子集.
设簇 $\mathsf{V}$ 中的代数均为 $\mathcal{F}$ 型的, 将 $G$ 中的元素作为 $0$ 元函数符号添加到 $\mathcal{F}$ 中, 对于 $\mathbf{G}$ 上的代数 $\mathbf{H}$, $h(g)$ 被看做 $\mathbf{H}$ 中的常数, 从而使得 $\mathsf{V}(\mathbf{G})$ 中的代数变为 $\mathcal{F}\cup G$ 型的代数, 显然 $\mathsf{V}(\mathbf{G})$ 是簇.
对于给定的变量集 $X$, 设 $\mathbf{F}(X)$ 为 $\mathsf{V}(\mathbf{G})$ 中的自由代数, 它同构于 $\mathsf{V}$ 中的自由代数 $\mathbf{F}_0(X)$ 和 $\mathbf{G}$ 的余积, 证明类似上一节多项式代数, 故不再重复.
如果从 $\mathbf{G}$ 到 $\mathbf{H}$ 的同态 $h$ 是单射, 则称 $\mathbf{H}$ 是忠实的, 显然 $\mathbf{G}$ 本身是忠实的, 自由代数 $\mathbf{F}(X)$ 也是忠实的. 所有忠实代数都将 $\mathbf{G}$ 当作其子代数.
代数集与根同余
本节内容建立在一般的簇上, 所以对于带常数的簇也成立.
给定簇 $\mathsf{V}$ 和有限变量集 $X$, 设 $\mathbf{F}(X)$ 为 $\mathsf{V}$ 中的自由代数, 定义 $\mathsf{V}$ 上的方程为二元有序对 $(p,q)$, $p,q\in F(X)$, 固定 $\mathsf{V}$ 中的一个代数 $\mathbf{H}$, 仿射空间定义为 $H^{\lvert X
vert}\cong\operatorname{Hom}{\mathsf{Set}}(X,H)\cong \operatorname{Hom}\mathsf{V}(\mathbf{F}(X),\mathbf{H})$, 方程 $(p,q)$ 在仿射空间中的根定义为点 $\mu\in\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 使得 $\mu(p)=\mu(q)$, 方程 $(p,q)$ 在仿射空间中的所有根定义为集合
\[Z((p,q))=\{\mu\in\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})\mid \mu(p)=\mu(q)\}.\]
对于 $F(X)\times F(X)=F(X)^2$ 的任一子集 $T$, 定义其零点集
\[Z(T)=\{\mu\in\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})\mid T\subseteq\ker\mu\},\]
其中 $\ker\mu$ 为之前定义的等价关系
\[\ker\mu = \{(p, q) \in F(X)^2 \mid \mu(p) = \mu(q)\}.\]
对于 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 的任一子集 $Y$, 定义其同余
\[I(Y)=\bigcap_{\mu\in Y}\ker\mu,\]
因为同态核一定是同余, 同余的交一定是同余, 故 $I(Y)$ 确为同余.
$Z(\cdot)$ 和 $T(\cdot)$ 给出仿射空间 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 的幂集与 $F(X)^2$ 的幂集之间的伽罗瓦连接, 对于仿射空间的子集 $Y$, 如果存在 $F(X)^2$ 的子集 $T$ 使得 $Y=Z(T)$, 则称其为代数集, 对于 $F(X)^2$ 的子集 $T$, 如果存在仿射空间的子集 $Y$ 使得 $T=I(Y)$, 则称其为根同余. 易证 $I(Z(I(Y)))=I(Y)$, $Z(I(Z(T)))=Z(T)$, 故全体代数集与全体根同余一一对应.
扎里斯基拓扑
定理
设 $I$ 是指标集, $\{T_i\}_{i\in I}$ 是一族 $F(X)^2$ 的子集, $\{Y_i\}_{i\in I}$ 是一族 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 的子集, 则以下关系成立:
$\mathrm{(1)}$ 若 $T_i\subseteq T_j$, 则 $Z(T_i)\supseteq Z(T_j)$;
$\mathrm{(2)}$ 若 $A_i\subseteq A_j$, 则 $I(Y_i)\supseteq I(Y_j)$;
$\mathrm{(3)}$ $\bigcap_{i\in I} Z(T_i)=Z\left(\bigcup T_j\right)$;
$\mathrm{(4)}$ $\bigcap_{i\in I} I(Y_i)=I\left(\bigcup Y_j\right)$;
$\mathrm{(5)}$ $\bigcup_{i\in I} Z(T_i)\subseteq Z\left(\bigcap T_j\right)$;
$\mathrm{(6)}$ $\bigcup_{i\in I} I(Y_i)\subseteq I\left(\bigcap Y_j\right)$.
这意味着代数集的任意交仍是代数集, 根同余的任意交仍是根同余, 但代数集的并未必是代数集, 根同余的并未必是根同余.
显然, $\operatorname{Hom}\mathsf{V}(\mathbf{F}(X),\mathbf{H})=Z(\Delta{F(X)})$, $\emptyset=Z(\nabla_{F(X)})$, 其中 $\Delta_{F(X)}$ 和 $\nabla_{F(X)}$ 是之前定义的平凡同余, 即 $F(X)^2$ 的对角线集和 $F(X)^2$ 本身, 这说明全集和空集是代数集.
定义(扎里斯基拓扑)
仿射空间 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 中的所有代数集和代数集的有限并组成 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 里的闭集, 这样得到的拓扑称为扎里斯基拓扑.
定理
设 $Y\subseteq\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$, $\overline{Y}$ 是 $Y$ 在扎里斯基拓扑下的闭包, 则 $\overline{Y}\subseteq Z(I(Y))$.
证明
显然 $Z(I(Y))$ 是代数集, 且它是包含 $Y$ 的最小代数集, 而 $\overline{Y}$ 未必是代数集, 故 $\overline{Y}\subseteq Z(I(Y))$.
定理
若 $Y\subseteq\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 且 $Y$ 在扎里斯基拓扑下是不可约集, 则 $\overline{Y}=Z(I(Y))$, 特别的, 不可约闭集是代数集.
证明
设 $\overline{Y}=\bigcap_{i\in I} Y_i$, 其中诸 $Y_i$ 是包含 $Y$ 的闭集, 设 $Y_i=\bigcup_{j\in J}Y_{i_j}$, 其中 $J$ 是有限指标集, 诸 $Y_{i_j}$ 是代数集, 故 $Y\subseteq\bigcup_{j\in J}Y_{i_j}$, 由于 $Y$ 不可约, 则存在某个 $j(i)\in J$, $Y\subseteq Y_{i_{j(i)}}$, 则 $\overline{Y}=\bigcap_{i\in I} Y_{i_{j(i)}}$, 故 $\overline{Y}$ 是代数集, 故 $\overline{Y}=Z(I(Y))$.
定义(代数簇)
不可约的代数集称为代数簇.
古典代数几何中代数集的有限并仍是代数集, 这是一个非常特殊的性质, 我们称之为整性.
定义(整性)
对于簇 $\mathsf{V}$ 中的代数 $\mathbf{H}$, 设 $Y_1$ 和 $Y_2$ 是 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 中任意两个代数集, 若 $Y_1\cup Y_2$ 仍为代数集, 则称代数 $\mathbf{H}$ 是整的.
这等价于说, 扎里斯基拓扑中闭集均为代数集, 代数闭域是整的, 此时扎里斯基拓扑便是古典代数几何中的扎里斯基拓扑.
显然代数集不一定是不可约的, 若代数集均可约, 则称代数 $\mathbf{H}$ 是余整的.
定义(余整)
对于簇 $\mathsf{V}$ 中的代数 $\mathbf{H}$, 若 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 中每个非空代数集在扎里斯基拓扑下都是不可约的, 则称代数 $\mathbf{H}$ 是余整的.
这等价于说代数集的有限并都不是代数集, 代数集都是代数簇.
诺特性
定义(等式诺特)
对于代数 $\mathbf{H}$, 若 $\mathbf{F}(X)$ 上任一同余 $T$ 都存在 $T$ 的有限子集 $S$, 使得 $Z(T)=Z(S)$, 则称 $\mathbf{H}$ 是等式诺特的.
定理
若簇 $\mathsf{V}$ 中自由代数 $\mathbf{F}(X)$ 是诺特代数, 则 $\mathsf{V}$ 中任意代数是等式诺特的.
证明
若 $\mathbf{F}(X)$ 是诺特的, 则 $\mathbf{F}(X)$ 上任一同余 $T$ 都存在 $T$ 的有限子集 $S$ 生成 $T$, 因 $S\subseteq T$, 则 $Z(T)\subseteq Z(S)$, 故 $I(Z(T))\supseteq I(Z(S))$, 因 $I(Z(S))$ 是包含 $S$ 的最小根同余, 而 $T$ 是包含 $S$ 的最小同余, 故显然 $I(Z(T))=I(Z(S))$, 从而有 $Z(T)=Z(S)$.
定理
等式诺特代数的子代数是等式诺特的.
证明
若 $\mathbf{H}$ 是等式诺特的, 则 $\mathbf{F}(X)$ 上任一同余 $T$ 都存在 $T$ 的有限子集 $S$, 使得 $Z(T)=Z(S)$, 若 $\mathbf{H}'$ 是 $\mathbf{H}$ 的子代数, 而 $Z(T)\cap\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H}')=Z(S)\cap\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H}')$, 故 $\mathbf{H}'$ 是等式诺特的.
回忆诺特空间的定义为满足闭集降链条件的空间, 可以证明关于等式诺特有以下定理.
定理
代数 $\mathbf{H}$ 是等式诺特的当且仅当对任意的有限变量集 $X$, $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 在扎里斯基拓扑下是诺特空间.
证明
见[3]Lemma 4.11.
定理
若 $\mathbf{H}$ 是等式诺特的, 则 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 中的代数集有唯一的不可约分解, 即若 $Y$ 是代数集且 $Y=\bigcup_{i=1}^n Y_i$, 诸 $Y_i$ 互不包含, 则这样的分解在不计诸 $Y_i$ 的顺序的意义下是唯一的.
证明
见[3]Theorem 4.12.
也就是说 $\mathbf{H}$ 是等式诺特时, 代数集有唯一的代数簇分解.
坐标代数
定义(坐标代数)
若 $Y$ 是 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 中的一个代数集, 则称 $\mathbf{F}(X)/I(Y)$ 为 $Y$ 的坐标代数, 记为 $A(Y)=\mathbf{F}(X)/I(Y)$ 为 $Y$ 的坐标代数.
显然自由代数 $\mathbf{F}(X)$ 是有限生成的, 它的生成集为 $X$, 而有限生成代数的商代数也是有限生成的, 故坐标代数都是有限生成的.
使用整性可以定义素同余.
定义(素同余)
设 $T$ 是 $\mathbf{F}(X)$ 上的同余, 若 $\mathbf{F}(X)/T$ 是整代数, 则称 $T$ 是一个素同余.
古典代数几何中素理想与代数簇一一对应, 下面是这个对应在泛代数几何中的版本.
定理
若 $\mathbf{H}$ 是整的, 则 $\operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$ 中的代数集 $Y$ 是代数簇当且仅当 $I(Y)$ 是一个素同余, 亦即其坐标代数 $A(Y)$ 是整代数.
证明
见[5]THEOREM 2.10.
坐标代数的另一作用是代数的展示.
定义
若 $X$ 是变量集, $\mathbf{F}(X)$ 是簇 $\mathsf{V}$ 中的自由代数, $T$ 是 $F(X)^2$ 的一个子集, 设 $N$ 为包含 $T$ 的最小同余, 则记 $\mathbf{F}(X)/N =\left \langle X\mid T \right \rangle $, 称为代数 $\mathbf{F}(X)/N $ 的一个展示. 若 $X$ 和 $T$ 是有限集, 则称 $\left \langle X\mid T \right \rangle $ 为有限展示.
显然自由代数有展示 $\langle X\mid\emptyset\rangle$.
当 $X$ 是有限集时, 展示 $\left \langle X\mid T \right \rangle $ 即为 $\mathbf{F}(X)/I(Z(T))$, 它是坐标代数 $A(Z(T))$, 而当 $Y$ 是代数集时, $A(Y)=\mathbf{F}(X)/I(Y)=\left \langle X\mid I(Y) \right \rangle$, 即坐标代数必有展示.
定理
若 $X$ 是有限变量集, $\mathbf{H}$ 是等式诺特的, 则任意有展示的代数都有有限展示.
证明
若 $\mathbf{H}$ 是等式诺特的, $T$ 是 $F(X)^2$ 的一个子集, 则存在 $T$ 的有限子集 $T'$ 使得 $Z(T)=Z(T')$, 故 $\left \langle X\mid T \right \rangle =\left \langle X\mid T' \right \rangle $.
每个簇中都有各自的字问题.
最后给出一个代数是坐标代数的充要条件.
定理
给定簇 $\mathsf{V}$ 中代数 $\mathbf{H}$, $\mathsf{V}$ 中一个代数 $\mathbf{C}$ 同构于某个非空代数集的坐标代数当且仅当 $\mathbf{C}$ 可以嵌入到 $\mathbf{H}$ 的某个积代数 $\mathbf{H}^I$ 中, 其中 $I$ 为指标集.
希尔伯特零点定理
在交换代数中, 理想的根可以定义为包含它的所有素理想的交, 希尔伯特零点定理告诉我们, 多项式环的一个理想 $T$ 的根也等于包含它的所有极大理想的交, 而这些极大理想又与 $Z(T)$ 中的点一一对应. 而在一般的簇中, $Z(T)$ 中的点并不和 $F(X)$ 的极大同余有一一对应关系, 我们在定义同余的根的时候应该寻找能与 $Z(T)$ 中的点建立一一对应的包含 $T$ 的某些同余, 而将 $T$ 的根定义为这些同余的交.
定理
若 $T$ 是 $\mathbf{F}(X)$ 上的同余, 则 $Z(T)$ 中的点与满足以下条件的同余 $S$ 一一对应: $T\subseteq S$ 且存在商代数 $\mathbf{F}(X)/S$ 到 $\mathbf{H}$ 的单射 $F(X)/S\to H$.
证明
对于任一 $\mu\in Z(T)$, 由 $Z(T)$ 的定义知 $T\subseteq \ker\mu$, 由第一同构定理知存在单射 $F(X)/\ker\mu\to H$, 故 $\ker\mu$ 即为包含 $T$ 且存在商代数到 $H$ 的单射的同余.
而对于包含 $T$ 且存在单射 $\iota\colon F(X)/S\to H$ 的同余 $S$, 设 $\pi\colon F(X)\to F(X)/S$ 是自然同态, 取 $\mu=\iota\circ\pi\in\operatorname{Hom}_{\mathsf{V}}(\mathbf{F}(X),\mathbf{H})$, 则 $S=\ker(\iota\circ\pi)=\ker\mu$, 由 $T\subseteq S=\ker\mu$ 知 $\mu\in Z(T)$.
定义(同余的根)
若 $T$ 是 $\mathbf{F}(X)$ 上的同余, $\pi$ 是 $F(X)\to F(X)/T$ 的自然同态, 则定义 $T$ 的根 $\sqrt{T}$ 为所有满足以下条件的同余 $T_i$ 的交, $T\subseteq T_i$ 且存在单射 $F(X)/T_i\to H$, 若 $\{T_i\}_{i\in I}$ 是所有这样的同余, 则 $\sqrt{T}=\bigcap_{i\in I}T_i$.
由同余的任意交仍是同余知 $\sqrt{T}$ 是同余, 且有 $T\subseteq\sqrt{T}$.
定理
若 $T$ 是 $\mathbf{F}(X)$ 上的同余, 则
$$
I(Z(T))=\sqrt{T}.
$$
证明
由 $I(\cdot)$ 的定义知
$$
I(Z(T))=\bigcap_{\mu\in Z(T)}\ker\mu,
$$
因为 $Z(T)$ 中的点与包含 $T$ 且存在商代数到 $\mathbf{H}$ 的单射的同余 $S$ 一一对应, 再由 $\sqrt{T}$ 的定义知
$$
\displaylines{
\bigcap_{\mu\in Z(T)}\ker\mu=\bigcap_{\substack{T\subseteq S\\ \text{存在单射}F(X)/S\to H}}S=\sqrt{T},
}
$$
结合两式便可得证.
定理
若 $T$ 是 $\mathbf{F}(X)$ 上的同余, 则存在 $Y\subseteq \operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$, 使得 $T=I(Y)$, 当且仅当 $T=\sqrt{T}$, 即 $T$ 是根同余当且仅当 $T=\sqrt{T}$.
证明
若存在 $Y\subseteq \operatorname{Hom}_\mathsf{V}(\mathbf{F}(X),\mathbf{H})$, 使得 $T=I(Y)$, 则由 $\sqrt{T}=I(Z(T))=I(Z(I(Y)))=I(Y)=T$ 得 $T=\sqrt{T}$. 反之, 若 $T=\sqrt{T}$, 则取 $Y=Z(T)$ 即可.
上述定理看似与希尔伯特零点定理形式类似, 但实际上, 将上述定理翻译到以代数闭域为常数的交换幺环簇上, 对应的版本是不依赖希尔伯特零点定理的, 但要说明这里定义的理想的根和根理想与古典代数几何中的一致需要希尔伯特零点定理. 在某些特定条件下有更好的性质.
定理
若 $\mathsf{V}$ 中任一有限生成代数的论域都是有限集, 设 $\mathbf{H}$ 是 $\mathsf{V}$ 中一个固定的代数, $\mathsf{V}$ 中某个代数集是代数簇当且仅当这个代数集的坐标代数可以嵌入到 $\mathbf{H}$ 中.
证明
见[14] Theorem 11.3.
设 $T$ 是 $F(X)$ 上的同余, 则 $Z(T)$ 是一个代数集, 设含于 $Z(T)$ 的代数簇为 ${Y_i}_{i\in I}$, 则 $I(Y_i)$ 是包含 $T$ 的同余, 其坐标代数为 $\mathbf{F}(X)/I(Y_i)$, 因此在上述定理的条件下, 一定存在单射 $F(X)/I(Y_i)\to H$. 反之, 每个包含 $T$ 且存在商代数到 $\mathbf{H}$ 的单射的同余都与含于 $Z(T)$ 的代数簇相对应. 如果 $\mathbf{H}$ 是整的, 则包含于 $Z(T)$ 的代数簇与包含 $T$ 的素同余一一对应, 故有以下定理.
定理
若 $\mathsf{V}$ 中任一有限生成代数的论域都是有限集, $\mathbf{H}$ 是 $\mathsf{V}$ 中整代数, 设 $T$ 是 $F(X)$ 上的同余, 那么 $\sqrt{T}$ 是包含 $T$ 的所有素同余的交.
显然上述定理中的条件不是最优的, 但姑且给出了交换代数中理想的根的性质的泛代数几何版本. 接下来转向含常数的簇, 通过推广代数闭的概念, 可以得到类似希尔伯特零点定理的定理, 即仿射空间中单点集与自由代数的极大理想的一一对应.
定义(代数闭)
若 $\mathbf{G}=(G,F)$ 是簇 $\mathsf{V}$ 中的一个对象, 设 $\mathbf{H}$ 是簇 $\mathsf{V}(\mathbf{G})$ 中的一个忠实代数, 若对任意有限变量集 $X$ 和 $\mathsf{V}(\mathbf{G})$ 中的自由代数 $\mathbf{F}(X)$ 的真同余 $T$, 对应的 $Z(T)$ 非空, 则称 $\mathbf{H}$ 是 $\mathbf{G}$-代数闭的.
定理(希尔伯特零点定理)
若 $\mathbf{G}=(G,F)$ 是簇 $\mathsf{V}$ 中的一个对象, $(\mathbf{H},h)$ 是带常数的簇 $\mathsf{V}(\mathbf{G})$ 中的一个忠实代数, $\mathbf{F}(X)$ 是 $\mathsf{V}(\mathbf{G})$ 中自由代数, 若 $\mathbf{H}$ 是 $\mathbf{G}$-代数闭的, 则 $\operatorname{Hom}_{\mathsf{V}(\mathbf{G})}(\mathbf{F}(X),\mathbf{H})$ 中的点与 $\mathbf{F}(X)$ 的极大同余一一对应.
证明
设 $\mu\in\operatorname{Hom}_{\mathsf{V}(\mathbf{G})}(\mathbf{F}(X),\mathbf{H})$, 设 $S$ 是包含 $I(\{\mu\})=\ker\mu$ 的同余, 则 $Z(S)$ 包含于 $Z(I(\{\mu\}))$, 考虑 $F(X)^2$ 的子集 $\{(x,\iota \circ h^{-1}\circ\mu(x))\}_{x\in X}$, 其中 $\iota\colon G\to F(X)$ 是自然嵌入, 由 $\mathbf{H}$ 和 $\mathbf{F}(X)$ 忠实性知 $\iota \circ h^{-1}\circ\mu(x)$ 是 $F(X)$ 中唯一确定的元素, 显然 $\{\mu\}=Z(\{(x,\iota \circ h^{-1}\circ\mu(x))\}_{x\in X})$, 故 $\{\mu\}$ 是代数集, 故 $Z(I(\{\mu\}))=\overline{\{\mu\}}=\{\mu\}$. 而又因为 $Z(S)$ 也是闭集, 则必有 $Z(S)=\emptyset$ 或 $Z(S)=\{\mu\}$, 若 $Z(S)=\emptyset$, 则由 $\mathbf{H}$ 的 $\mathbf{G}$-代数闭性知 $S$ 不是真同余, 则显然 $S=F(X)^2$, 故知 $I(\{\mu\})$ 是极大同余.
若 $\mathfrak{m}$ 是 $\mathbf{F}(X)$ 中的极大同余, 则 $Z(\mathfrak{m})$ 非空, 设 $\mu\in Z(\mathfrak{m})$, 则 $I(\{\mu\})$ 包含 $I(Z(\mathfrak{m}))=\sqrt{\mathfrak{m}}$, 因 $\mathfrak{m}$ 极大, 则必有 $\sqrt{\mathfrak{m}}=\mathfrak{m}$ 或 $\sqrt{\mathfrak{m}}=F(X)$, 若 $\sqrt{\mathfrak{m}}=F(X)$, 则与 $I(\{\mu\})$ 极大矛盾, 若 $\sqrt{\mathfrak{m}}=\mathfrak{m}$, 则由 $I(\{\mu\})$ 极大知 $I(\{\mu\})=\mathfrak{m}$, 故 $\{\mu\}=Z(I(\{\mu\}))=Z(\mathfrak{m})$.
定理
若 $\mathbf{G}$ 是簇 $\mathsf{V}$ 中的一个对象, $\mathbf{H}$ 是带常数的簇 $\mathsf{V}(\mathbf{G})$ 中的一个忠实 $\mathbf{G}$-代数闭整代数, $\mathbf{F}(X)$ 是 $\mathsf{V}(\mathbf{G})$ 中自由代数, 则 $\mathbf{F}(X)$ 的极大同余都是素同余.
证明
由 $\mathbf{H}$ 的忠实性和 $\mathbf{G}$-代数闭性知 $\mathbf{F}(X)$ 的极大同余与 $\operatorname{Hom}_{\mathsf{V}(\mathbf{G})}(\mathbf{F}(X),\mathbf{H})$ 中的点一一对应, 而 $\operatorname{Hom}_{\mathsf{V}(\mathbf{G})}(\mathbf{F}(X),\mathbf{H})$ 中的点显然都是不可约的, 上个定理的证明中已经说明这些单点集都是代数集, 则它们是代数簇, 由 $\mathbf{H}$ 的整性知它们对应的同余都是素同余, 故极大同余都是素同余.
新问题
将古典代数几何中的更多概念, 定理或性质翻译为泛代数几何的版本固然是一个研究方向, 但泛代数几何并不局限于此, 而是在其发展的过程中产生了许多新问题, 本节叙述这些新问题.
定义(代数集的范畴)
设 $\mathbf{H}$ 是簇 $\mathsf{V}$ 中的一个代数, 定义代数集的范畴为 $\mathsf{K}_{\mathsf{V}}(\mathbf{H})$, 其中对象为有序对 $(X,A)$, 其中 $X$ 是任意有限集, $A$ 是 $\operatorname{Hom}_{\mathsf{V}}(\mathbf{F}(X),\mathbf{H})$ 中代数集. 对象间的态射也是一个有序对 $(f,f_*)\colon(X,A)\to(Y,B)$, 其中 $f$ 为满足如下条件的集合间映射 $X\to Y$: 由 $f$ 自然的诱导出自由代数间同态 $\bar f\colon F(X)\to F(Y)$, 对于 $A$ 中任一元素 $\mu\in A\subseteq\operatorname{Hom}_{\mathsf{V}}(\mathbf{F}(X),\mathbf{H})$, 有 $\bar f\circ\mu\in B\subseteq\operatorname{Hom}_{\mathsf{V}}(\mathbf{F}(Y),\mathbf{H})$. 由此诱导出代数间态射 $f_*\colon A\to B,\mu\mapsto \bar f\circ\mu$, 容易验证由此定义的 $\mathsf{K}_{\mathsf{V}}(\mathbf{H})$ 确为范畴.
范畴 $\mathsf{K}{\mathsf{V}}(\mathbf{H})$ 有两个参数, 首先可以考虑改变簇, 若 $\mathsf{V}_1$ 和 $\mathsf{V}_2$ 是簇, 其中代数都是同型的, 且代数 $\mathbf{H}$ 同时在这两个簇中, 研究 $\mathsf{K}{\mathsf{V}1}(\mathbf{H})$ 和 $\mathsf{K}{\mathsf{V}2}(\mathbf{H})$ 的关系, 特别的, 可以研究带不同常数的簇 $\mathsf{K}{\mathsf{V}(\mathbf{G_1})}(\mathbf{H})$ 和 $\mathsf{K}_{\mathsf{V}(\mathbf{G_2})}(\mathbf{H})$ 之间的关系, 其中 $\mathbf{G}_1$ 和 $\mathbf{G}_2$ 是 $\mathsf{V}$ 中的代数.
还可以改变 $\mathbf{H}$, 设 $\mathbf{H}1$ 和 $\mathbf{H}_2$ 是 $\mathsf{V}$ 中的代数, 研究 $\mathsf{K}{\mathsf{V}}(\mathbf{H}1)$ 和 $\mathsf{K}{\mathsf{V}}(\mathbf{H}2)$ 之间的关系, 特别的, 对于固定的代数 $\mathbf{G}$, 可以研究 $\mathsf{K}{\mathsf{V}(\mathbf{G})}(\mathbf{H}1)$ 和 $\mathsf{K}{\mathsf{V}(\mathbf{G})}(\mathbf{H}_2)$ 之间的关系.
设 $T\subseteq F(X)^2$, 在 $\mathsf{K}{\mathsf{V}}(\mathbf{H}_1)$ 中的 $Z(T)$ 记作 $Y_1$, 在 $\mathsf{K}{\mathsf{V}}(\mathbf{H}_1)$ 中的 $Z(T)$ 记作 $Y_2$, 若 $I(Y_1)=I(Y_2)$, 则称 $\mathbf{H}_1$ 和 $\mathbf{H}_2$ 是 $\mathsf{V}$ 是几何等价的. 显然, 若 $\mathbf{G}$ 是 $\mathbf{G}$-代数闭的, 则在 $\mathsf{V}(\mathbf{G})$ 中, 如果 $\mathbf{H}_1$ 和 $\mathbf{H}_2$ 都是忠实的, 则他们几何等价.
这两类问题的进一步研究可见参考文献.
特定簇上的代数几何也是一个研究方向, 毕竟特定簇具有更好的性质, 比如群上的代数几何, 李群上的代数几何等方向都取得了很多有趣的成果.
关于泛代数几何的进一步了解可以参看综述[14]及其参考文献.
参考文献
[1] Clifford Bergman, Universal algebra: Fundamentals and selected topics, 1 ed., Chapman and Hall/CRC, 2011.
[2] S. Burris and H.P. Sankappanavar, A course in universal algebra, Graduate Texts in Mathematics, vol. 78, Springer New York, 1981.
[3] E. Yu. Daniyarova, A. G. Myasnikov, and V. N. Remeslennikov, Unification theorems in algebraic geometry, Algebra and Discrete Mathematics 1 (2008), 80–111.
[4] E. Yu. Daniyarova, A. G. Myasnikov, and V. N. Remeslennikov, Algebraic geometry over algebraic structures III: Equationally noetherian property and compactness, South. Asian Bull. Math. 35, no. 1 (2011), 35–68.
[5] E. Yu. Daniyarova, A. G. Myasnikov, and V. N. Remeslennikov, Algebraic geometry over algebraic structures. IV. Equational domains and codomains, Algebra and Logic 49, no. 6 (2011), 483–508.
[6] E. Yu. Daniyarova, A. G. Myasnikov, and V. N. Remeslennikov, Algebraic geometry over algebraic structures. II. Foundations, J. Math. Sci. 185, no. 3 (2012), 389–416.
[7] E. Yu. Daniyarova, A. G. Myasnikov, and V. N. Remeslennikov, Algebraic geometry over algebraic structures. V. The case of arbitrary signature, Algebra and logic 51, no. 1 (2012), 28–40.
[8] Robin Hartshorne, Algebraic geometry, Graduate Texts in Mathematics, vol. 52, Springer-Verlag, 1977.
[9] B. Plotkin, Varieties of algebras and algebraic varieties, Izrael J. Math. 96, no. 2 (1996), 511–522.
[10] B. Plotkin, Varieties of algebras and algebraic varieties. Categories of algebraic varieties, Siberian Advances in Math. 7, no. 2 (1997), 64–97.
[11] B. Plotkin, Seven lectures on the universal algebraic geometry, 2002.
[12] B. Plotkin, Algebraic logic, varieties of algebras and algebraic varieties, 2003.
[13] B. Plotkin, Algebras with the same (algebraic) geometry, Proc. Steklov Inst. Math. 242 (2003), 165–196.
[14] Artem N. Shevlyakov, Lectures notes in universal algebraic geometry, arXiv: Algebraic Geometry (2016).
[15] 冯琦, 数理逻辑引导, 科学出版社, 2017.
[16] 李文威, 代数学方法: 卷一, 高等教育出版社, 2019.
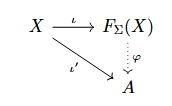
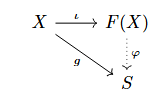 由余积的泛性质, 对于环 $S$ 和环同态 $\varphi\colon F(X)\to S$, 有唯一的环同态 $\psi$ 使下图交换,
由余积的泛性质, 对于环 $S$ 和环同态 $\varphi\colon F(X)\to S$, 有唯一的环同态 $\psi$ 使下图交换,
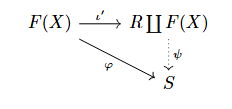 将两图连接即得交换图
将两图连接即得交换图
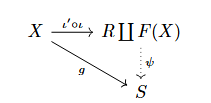 若 $S$ 同时为 $R$-代数, 该图依然成立, 便知 $R\coprod F(X)$ 为 $R$-$\mathsf{CAlg}$ 中的自由对象, 由自由对象唯一性知 $R\coprod F(X)$ 与 $R[X]$ 同构.
若 $S$ 同时为 $R$-代数, 该图依然成立, 便知 $R\coprod F(X)$ 为 $R$-$\mathsf{CAlg}$ 中的自由对象, 由自由对象唯一性知 $R\coprod F(X)$ 与 $R[X]$ 同构.