多项式列
设 $\{p_n(x)\}_{n=0}^\infty$ 是一列 $\mathbb{C}[x]$ 中的多项式, 以后我们说的多项式列都要求有 $ \deg p_n=n $, 即第 $ n $ 个多项式的次数恰好为 $ n $, 其中当 $ n=0 $ 时解释为非零常函数 ( $ p(x)=0 $ 的次数通常定义为无穷小 ). 显然这样的一列多项式组成线性空间 $ \mathbb{C}[x] $ 的一组基.
显然有 $ p_0(x)=1 $, 当 $ n $ 为正整数时有 $ p_n(0)=0 $.
二项式型多项式的例子有: $ x^n $, 上升阶乘 $ (x)^n=x(x+ 1)\cdots (x + n - 1) $, 下降阶乘 $ (x)_n=x(x-1)\cdots (x - n + 1) $, 阿贝尔多项式 $ x(x-an)^{n-1} $, 贝尔多项式等.
设其指数型生成函数是
\[G(x,t)=\sum_{n=0}^\infty p_n(x)\frac{t^n}{n!},\]则有函数方程 $ G(x+y,t)=G(x,t)G(y,t) $, 可以证明以下定理:
设其指数型生成函数是 $ G(x,t) $, 则有微分方程 $ \frac{\mathrm{d}}{\mathrm{d}x}G(x,t)=tG(x,t) $, 于是有
展开生成函数即可得到阿佩尔多项式列中多项式的具体表达式为
\[p_n(x)=\sum_{k=0}^n\binom{n}{k}k!A_{k}x^{n-k}.\]阿佩尔多项式的例子有: $ x^n $, 伯努利多项式, 赫尔米特多项式, 欧拉多项式等.
显然二项式型多项式列和阿佩尔多项式列均为特殊的谢弗多项式列.
任何一个多项式列都可以对应一个无穷大的下三角矩阵, 定义 $\{p_n(x)\}{n=0}^\infty$ 对应的下三角无穷矩阵为 $ (a{nk}) $, 即
\[\begin{pmatrix} a_{0,0} & 0 & 0 & 0 & \cdots \\ a_{1,0} & a_{1,1} & 0 & 0 & \cdots \\ a_{2,0} & a_{2,1} & a_{2,2} & 0 & \cdots \\ a_{3,0} & a_{3,1} & a_{3,2} & a_{3,3} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix}\]该矩阵称为Riordan矩阵, 无穷大矩阵的乘积按通常矩阵乘法推广, 显然两个多项式的哑复合为他们对应的矩阵的乘积 $ (a_{nk})(b_{nk}) $ 对应的多项式, 因为 $ p_n $ 是 $ n $ 次多项式, 故矩阵对角线元都不是 $ 0 $, 由矩阵乘法知哑复合运算是结合的和可逆的(逆元称为共轭多项式列), 并且有单位元 $ \{x^n\}_{n=0}^\infty $, 哑复合一般不是可交换的. 全体二项式型多项式列组成的集合, 全体阿佩尔多项式列组成的集合以及全体谢弗多项式列组成的集合在该运算下均是群, 分别记为 $ \mathbb{B} $, $ \mathbb{A} $ 和 $ \mathbb{S} $, 分别称为阿佩尔子群, 拉格朗日子群和Riordan群. $ \mathbb{B} $ 和 $ \mathbb{A} $ 均是 $ \mathbb{S} $ 的子群, 其中 $ \mathbb{A} $ 还是阿贝尔子群和正规子群, 并且有 $ \mathbb{S}=\mathbb{A}\rtimes\mathbb{B} $.
如果 $\{p_n(x)\}{n=0}^\infty$ 和 $\{q_n(x)\}{n=0}^\infty$ 的生成函数分别是 $ A(t)e^{xB(t)} $ 和 $ C(t)e^{xD(t)} $, 可以验证, $ \{(p\circ q)n(x)\}{n=0}^\infty $ 的生成函数是 $ A(t)C(B(t))e^{xD(B(t))} $.
谢弗多项式列之上还有广义阿佩尔多项式列和Boas-Buck多项式列等推广, 但我们此处不涉及它们.
泛函
设 $ P=\mathbb{C}[x] $ 为多项式代数, 定义 $ P^* $ 为其上所有线性泛函组成的集合, 即对偶空间.
设 $ L\in P^* $, $ p(x)\in P $, 泛函在多项式上的作用写作
\[\langle L \mid p(x) \rangle,\]这借鉴自物理学中的狄拉克符号,
设数列 $ \{a_n\}_{n=0}^\infty $ 的指数型生成函数是
\[f(t) = \sum_{k=0}^{\infty} \frac{a_k}{k!} t^k,\]定义它对应的线性泛函为 $ \langle A \mid x^n \rangle=a_n, $ 称 $ A $ 为该数列对应的哑元, 在经典哑演算中, 也写作 $ A^n=a_n $, 对应经典哑演算将下标移为上标的操作.
设 $ \mathbb{C}[[t]] $ 为以 $ t $ 为变量的形式幂级数代数, 对于 $ L\in P^* $, 定义映射
\[L\mapsto f_L(t)=\sum_{k=0}^{\infty} \frac{\langle L \mid x^k \rangle}{k!} t^k,\]由前面的讨论知该映射是双射, 并且显然保持线性空间的结构, 因此它是从 $ P^* $ 到 $ \mathbb{C}[[t]] $ 的线性同构, 此后将两者看做同一. 先来看一些简单的性质.
接下来举几个例子.
取 $ f(t)=t^k $, 则 $ \langle t^k \mid x^n \rangle=\frac{\delta_{k,n}}{n!} $, 从而有 $ \langle t^k \mid p(x) \rangle=p^{(k)}(0) $.
取 $ f(t)=e^{yt} $, 则 $ \langle e^{yt} \mid x^n \rangle=y^n $, 从而有 $ \langle e^{yt} \mid p(x) \rangle=p(y) $, 因此称为取值泛函, 显然 $ \langle e^{yt}-1 \mid p(x) \rangle=p(y)-p(0) $.
取 $ f(t)=te^{yt} $, 则 $ \langle te^{yt} \mid x^n \rangle=ny^{n-1} $, 从而有 $ \langle te^{yt} \mid p(x) \rangle=p'(y) $, 进而 $ \langle t^ke^{yt}-1 \mid p(x) \rangle=p^{(k)}(y) $.
取 $ f(t)=(1 - t)^{-1} $, 则 $ \langle (1 - t)^{-1} \mid x^n \rangle=n! $, 因为 $ n!=\int_0^\infty u^ne^{-u}\mathrm{d}u $, 从而有 $$ \langle (1 - t)^{-1} \mid p(x) \rangle=\int_0^\infty p(u)e^{-u}\mathrm{d}u. $$ 取 $ f(t)=\frac{e^{yt}-1}{t} $, 则 $$ \langle \frac{e^{yt}-1}{t} \mid p(x) \rangle=\int_0^y p(u)\mathrm{d}u, $$ 称为积分泛函.
取 $ f(t)=\frac{t}{e^t-1} $, 它是积分泛函的逆泛函, 设它对应的哑元为 $ B $, 则 $ \langle B \mid x^n \rangle=B_n $ 为伯努利数 经典哑演算中写作 $ B^n=B_n $.
取 $ f(t)=\frac{1 + e^{yt}}{2} $, 则 $$ \left\langle \frac{1 + e^{yt}}{2} \bigg\lvert p(x) \right\rangle = \frac{p(0) + p(y)}{2}, $$ 它的逆是 $ f(t)=\frac{2}{1 + e^{t}} $, 设它对应哑元为 $ E $, 则 $ \langle E \mid x^n \rangle=E_n $ 是欧拉多项式在 $ 0 $ 处的值, 也叫欧拉数.
线性变换
接下来我们把 $ P^* $ 中的元素做成 $ P $ 上的线性变换, 设 $ f_L(t)=\sum_{k=0}^{\infty} \frac{\langle L \mid x^k \rangle}{k!} t^k $, 再设 $ \langle L \mid x^k \rangle=L_k $, 定义 $ f_L(t) $ 的左乘作用为
\[f_L(t)\cdot x^n=\sum_{k=0}^{n}\binom{n}{k} L_kx^{n-k},\]这定义了一个 $ P\to P $ 的线性变换, 称它为由级数 $ f_L(t) $ 生成的线性变换.
如果 $ P $ 上的线性变换将 $ n $ 次多项式映为 $ n $ 次多项式, 则它显然是线性同构, 如果它还由 $ f_L(t) $ 生成, 则显然有 $ L_0=f_L(0)\neq0 $.
设 $ f(t)=t $, 则 $ t\cdot p(x)=p'(x) $, 因此也称其为微分变换或微分算子, 记其哑元为 $ D $, 因此形式上有 $$ e^{yt}=e^{yD}, $$ 并且 $ e^{yD}\cdot p(x)=p(x+y) $, 左边展开为级数就得到了 $ p $ 在 $ x $ 处的泰勒级数, 因为 $ p $ 是多项式, 这里不必考虑收敛问题, 这就是经典哑演算中 $ e^{\frac{\mathrm{d}}{\mathrm{d}x}} $ 的意义.
更多的例子: $$ t^ke^{yt}\cdot p(x)=p^{(k)}(x+y), $$ $$ (1 - t)^{-1} \cdot p(x)=\int_0^\infty p(x+u)e^{-u}\mathrm{d}u, $$ $$ \frac{e^{yt}-1}{t}\cdot p(x)=\int_x^{x+y} p(u)\mathrm{d}u, $$ $$ \frac{t}{e^t-1}\cdot x^n=B_n(x) $$ 为伯努利多项式, 这对应经典哑演算中 $ (B+x)^n=B_n(x). $ $$ \frac{1 + e^{yt}}{2}\cdot p(x)=\frac{p(x)+p(x+y)}{2}, $$ $$ \frac{2}{1 + e^{t}}\cdot x^n= E_n(x) $$ 为欧拉多项式.
设 $ T(x^n)=p_n(x) $ 为阿佩尔多项式列, 则它的生成函数为 $ A(t)e^{xt} $ 的形式, 其中 $ A(t)=\sum_{k=0}^\infty A_kx^k $ 为常数项非零的幂级数, 则 $$ A(t)\cdot x^n=\sum_{k=0}^n\binom{n}{k}A_kk!x^{n-k}=p_n(x), $$ 第一个等号是左乘作用的定义, 第二个等号是之前得到的阿佩尔多项式列的具体形式, 所以由 $ A(t) $ 就可以生成 $ T $.
设阿佩尔多项式列 $ {p_n(x)} $ 的指数型生成函数是
\[G(x,t)=\sum_{n=0}^\infty p_n(x)\frac{t^n}{n!},\]则
\[G(0,t)\cdot x^n=p_n(x),\]将 $ G(x,t) $ 解释为含参数 $ x $ 的泛函 $ \mathbb{C}[y]\to\mathbb{C} $ 时, 有
\[\langle G(x,t)\mid y^n\rangle=p_n(x),\]所以
\[p_n(x)=\langle G(x,t)\mid y^n\rangle=G(0,t)\cdot x^n=\sum_{k=0}^n\binom{n}{k}\langle G(0,t)\mid y^n\rangle x^{n-k}=\langle G(0,t)\mid (x+y)^n\rangle,\]在经典哑演算中, 设 $ P $ 是数列 $ {p_n(0)} $ 的哑元, 则上式就解释为
\[p_n(x)=\sum_{k=0}^n\binom{n}{k}p_k(0)x^{n-k}=\sum_{k=0}^n\binom{n}{k}P^kx^{n-k}=(x+P)^n.\]另一方面,
\[\sum_{k=0}^n\binom{n}{k}\langle G(0,t)\mid y^n\rangle x^{n-k}=\langle G(0,t)\mid (x+y)^n\rangle\]等价于说
\[\sum_{k=0}^n\binom{n}{k}p_n(y) x^{n-k}=p_n(x+y),\]这个式子称为阿佩尔恒等式.
接下来介绍谢弗多项式列的另一种定义.
事实上, 如果 $ \langle g(t)\left(f(t)\right)^k\mid p_n(x)\rangle=n!\delta_{nk}, $ 那么 $ p_n(x) $ 的生成函数就是
\[\sum_{n=0}^\infty p_n(x)\frac{t^n}{n!}=\frac{1}{g(\bar f(t))}e^{x\bar{f}(t)},\]其中 $ f(\bar{f}(t))=\bar{f}(f(t))=t. $
算子与伴随算子
举两个例子.
伴随算子的定义与通常泛函分析中相同.
$ (\tau + \sigma)^\times = \tau^\times + \sigma^\times, $
若 $ r \in \mathbb{C} $, $ (r\tau)^\times = r\tau^\times , $
$ (\tau\sigma)^\times = \sigma^\times\tau^\times, $
若 $ \tau $ 可逆, $ (\tau^{-1})^\times = (\tau^\times)^{-1} . $
举一个例子,
\[\delta_{1n}=\langle1\mid x^n\rangle=\left\langle\frac{e^t-1}{t}\frac{t}{e^t-1}\bigg\lvert x^n\right\rangle=\left\langle\frac{e^t-1}{t}\bigg\lvert\frac{t}{e^t-1}\cdot x^n\right\rangle\] \[=\left\langle\frac{e^t-1}{t}\bigg\lvert B_n(x)\right\rangle=\int_0^1 B_n(x)\mathrm{d}x,\]其中 $ B_n(x) $ 是伯努利多项式, 这就是伯努利多项式的积分性质, 另一方面,
\[\delta_{1n}=\langle1\mid x^n\rangle=\left\langle\frac{t}{e^t-1}\frac{e^t-1}{t}\bigg\lvert x^n\right\rangle=\left\langle\frac{t}{e^t-1}\bigg\lvert\frac{e^t-1}{t}\cdot x^n\right\rangle=\left\langle\frac{t}{e^t-1}\bigg\lvert\int_x^{x+1}u^n\mathrm{d}u\right\rangle\] \[=\left\langle\frac{t}{e^t-1}\bigg\lvert\frac{(x+1)^{n+1}-x^{n+1}}{n+1}\right\rangle=\frac{1}{n+1}\sum_{k=0}^{n}\binom{n+1}{k}B_k,\]这就是伯努利数的递推公式.
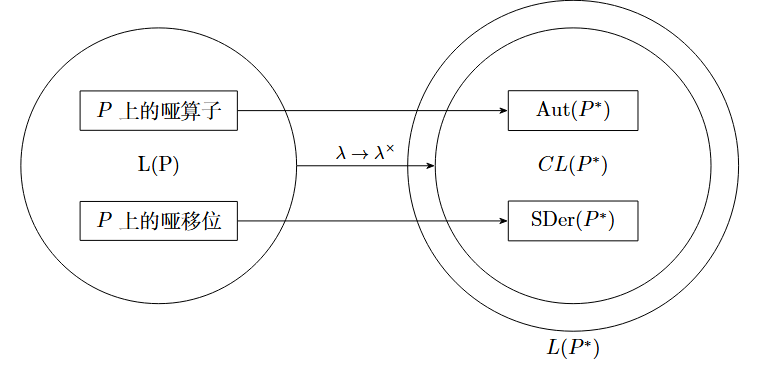
既然伴随 $ \times $ 是从 $ L(P) $ 到 $ L(P^*) $ 中所有连续算子组成的子空间的同构, 自然的想法是考虑该映射下 $ L(P) $ 中各种类型元素的对应关系, 事实上, 先前介绍的 $ L(P) $ 中两类重要的算子, 哑算子和哑移位, 在该映射下的像恰好分别是 $ P^* $ 上自同构算子和满导数算子.
假设 $ \lambda\in L(P) $ 将 $ x^n $ 映为 $ p_n(x) $, $ {p_n(x)} $ 是二项式型多项式列, 并且有 $ f(t)\in P^* $,
\[\langle \left(f(t)\right)^k\mid p_n(x)\rangle=n!\delta_{nk}\]对任意非负整数 $ n $ 和 $ k $ 成立, 此后将明确了 $ f $ 的哑算子 $ \lambda $ 记为 $ \lambda_f $.
设 $ \lambda_f $ 和 $ \lambda_g $ 是哑算子, 并且 $ \lambda_f(x^n)=p_n(x) $, $ \lambda_g(x^n)=q_n(x) $, 则它们的复合 $ \lambda_f\circ\lambda_g(x^n)=\lambda_fq_n(x)=(q\circ p)n(x) $ 是哑复合, 先前已说明二项式型多项式列在哑复合下构成群, 所以哑算子在算子复合下也构成群, 并且与 $ \mathbb{B} $ 同构.另一方面, 还有 $ \lambda_f\circ\lambda_g=\lambda{g\circ f} $, 其中下标是幂级数的复合, 这是因为二者的生成函数分别是 $ e^{x\bar{f}(t)} $ 和 $ e^{x\bar{g}(t)} $, 哑复合的生成函数就是 $ e^{x\bar{f}(\bar{g}(t))}=e^{x\overline{g\circ f}(t)} $, 其中 $ \bar{f} $ 是 $ f $ 的复合逆, 所以还有 $ \lambda_f^{-1}=\lambda_{\bar{f}} $.
因为谢弗多项式列在哑复合下也构成群, 所以谢弗算子在算子下也构成群, 并且同构于 $ \mathbb{S} $.假设 $ \lambda\in L(P) $ 将 $ x^n $ 映为 $ p_n(x) $, $ {p_n(x)} $ 是谢弗多项式列, 并且有 $ f(t),g(t)\in P^* $,
\[\langle g(t)\left(f(t)\right)^k\mid p_n(x)\rangle=n!\delta_{nk}\]对任意非负整数 $ n $ 和 $ k $ 成立, 此后将明确了 $ f $ 和 $ g $ 的谢弗算子 $ \lambda $ 记为 $ \lambda_{f,g} $, 由生成函数易知有
\[\lambda_{f,g}=\frac{1}{g(t)}\circ\lambda_{1,f}=\frac{1}{g(t)}\circ\lambda_f,\]即谢弗算子一定与哑算子差一个由可逆幂级数定义的线性算子, 并且有
\[\lambda_{f,g}\circ\lambda_{h,k}=\lambda_{g\cdot h\circ f,k\circ f},\]其中 $ \circ $ 是幂级数复合, $ \cdot $ 是幂级数乘法, 故有 $ \lambda_{f,g}^{-1}=\lambda_{\frac{1}{g}\circ\bar{f},\bar{f}} $.
与之类似, 可以证明如下定理:
如果哑移位 $ \theta (p_n(x))=p_{n+1}(x) $, 有 $ \langle \left(f(t)\right)^k\mid p_n(x)\rangle=n!\delta_{nk} $ 成立时将其记为 $ \theta_f $, 有 $ \langle g(t)\left(f(t)\right)^k\mid p_n(x)\rangle=n!\delta_{nk} $ 成立时则记作 $ \theta_{f,g} $, 那么有
\[\theta_f^\times(f(t)^k)=kf(t)^{k-1}\]对所有正整数 $ k $ 成立, 还有
\[\theta_{f,g}=\frac{1}{g(t)}\theta_f(g(t))\]伴随 $ \times $ 将所有哑移位组成的集合映为所有满导数算子组成的集合, 一般记 $ \theta_f^\times=D_f $.
例如, 如果 $ \theta_t(x^n)=x^{n+1} $, 那么记 $ \theta^\times_t=D_t $, 有
\[f'(t)=D_t(f(t))=f(t)\circ\theta_t-\theta_t\circ f(t)=f(t)\circ x-x\circ f(t),\]两边均为 $ P $ 上的算子, 最后一个等号是因为 $ \theta_t $ 作用在多项式上等价于给多项式乘 $ x $.
若 $ \theta_{f,g} $ 是谢弗移位, 则有
\[\theta_{f,g}=\frac{1}{g(t)}\circ\theta_f\circ g(t).\]总结
哑演算的理论并不是解释为什么哑演算有时是正确的, 而是找出哑演算在什么时候是正确的, 我们工作的主要舞台是复数域(实际上可以是任意域)上的一元多项式代数 $ \mathbb{C}[x] $(因此不需要考虑收敛), 简写为 $ \mathbb{C}[x]=P $, $ P $ 的对偶空间, 也就是所有线性泛函组成的空间, 同构于复数域上的形式幂级数代数 $ \mathbb{C}[[t]] $, 即 $ P^*\cong\mathbb{C}[[t]] $, 其中的形式幂级数
\[f(t) = \sum_{k=0}^{\infty} \frac{a_k}{k!} t^k\]有两种功能, 一种是作为线性泛函, 写作
\[\langle f(t)\mid x^n\rangle=a_n,\]另一种是作为 $ P $ 上的线性变换, 也就是将 $ \mathbb{C}[[t]] $ 看作 $ L(P) $ 的子集, 写作左乘作用
\[f(t)\cdot x^n=\sum_{k=0}^{n}\binom{n}{k} a_kx^{n-k},\]这里我们仅写了在 $ x^n $ 上作用的结果, 因为 $ {x^n} $ 是 $ P $ 的一组基, 由线性性, 知道在它们上的作用结果就能确定在 $ P $ 里任意多项式上的作用结果, 二者以
\[\langle f(t)\mid p(x)\rangle=\langle1\mid f(t)\cdot p(x)\rangle\]相关联.
接下来考察 $ P $ 上线性变换 $ \lambda $ 在 $ x^n $ 上的像, 假设 $ \lambda(x^n)=p_n(x) $, 我们重点关注 $ {p_n(x)} $ 分别是阿佩尔多项式列, 二项式型多项式列和谢弗多项式列的情形, 其中前二者是后者的子集.
有两种方式生成 $ P $ 上的线性变换, 第一种是 $ \lambda(x^n)=f(t)\cdot x^n=p_n(x) $, 线性变换将 $ x^n $ 映为阿佩尔多项式列当且仅当该线性变换可以由这种方式生成, 其中 $ f(t) $ 是这个阿佩尔多项式列的生成函数 $ f(t)e^{xt} $ 在 $ x=0 $ 处的值. 全体阿佩尔多项式列组成的集合记作 $ \mathbb{A} $, 它在加法, 数乘和哑复合下构成一个 $ \mathbb{C} $ 代数, 它与全体可逆幂级数在加法, 数乘和乘法下构成的 $ \mathbb{C} $ 代数同构, 也与全体将 $ x^n $ 映为阿佩尔多项式列的线性变换在加法, 数乘和复合构成的 $ \mathbb{C} $ 代数同构. 对于将 $ x^n $ 映为阿佩尔多项式列 $ B_n(x) $ 的线性变换, 记
\[B^n=\langle f(t)\mid x^n\rangle=\langle1\mid f(t)\cdot x^n\rangle=\langle1\mid p_n(x)\rangle=B_n(0),\]称 $ B=B^1 $ 为这个阿佩尔多项式列对应的哑元, 显然有
\[B^nB^m=\langle f(t)\mid x^{n+m}\rangle=B^{n+m},B^n+B^m=\langle f(t)\mid x^n+x^m\rangle,\]哑元的数乘定义为 $ (kB)^n=\langle kf(t)\mid x^n\rangle=kB^n $, 哑元间加法定义为 $ (B+E)^n=\langle f(t)+g(t)\mid x^n\rangle=B^n+E^n $, 哑元之间的乘法定义为 $ (BE)^n=(EB)^n=\langle f(t)g(t)\mid x^n\rangle $, 哑元在加法, 数乘和乘法下构成一个 $ \mathbb{C} $ 代数, 并且也与 $ \mathbb{A} $ 同构, 即有交换代数同构
\[\mathbb{A}\cong(P^*,+,\cdot)^\times\cong\left(\{\lambda:x^n\mapsto p_n(x) | p_n(x)\text{是阿佩尔多项式列}\},+,\circ\right)\cong\left(\{B|B\text{是哑元}\},+,\cdot\right).\]对于多项式 $ p(x)=\sum_{n=0}p_nx^n\in P $, 定义 $ p(B)=\sum_{n=0}p_nB^n $, 对任意哑元可以定义哑元代数上的一个算子, 例如 $ B $ 对应的算子依然记为 $ B $, 作用在 $ E $ 上得到的就是
\[B(E)=BE, B(E^n)=(BE)^n,\]如果 $ B^n=\langle 1\mid f(t)\cdot x^n\rangle $, 那么 $ B(p(E))=p(BE)=[f(t)\cdot p(x)]_{x=E} $.
举几个例子, 如果哑元 $ V_y $ 由 $ f_y(t)=e^{yt} $ 定义, 那么 $ f_y(t)\cdot p(x)=p(x+y) $, 故 $ V_y(E^n)=(E+y)^n=E_n(y) $ 对任意哑元 $ E $ 和任意正整数 $ n $ 成立.
如果哑元 $ D $ 由 $ f(t)=t $ 定义, 那么 $ f(t)\cdot p(x)=p’(x) $, 故 $ D(E^n)=nE^{n-1} $ 对任意哑元 $ E $ 和任意正整数 $ n $ 成立. 将 $ V_y $ 和 $ D $ 复合, 就有 $ nE_{n-1}(y)=(V_yD)(E^n)=(DV_y)(E^n)=E_n’(y) $.
如果哑元 $ \Delta $ 由 $ f(t)=e^t-1 $ 定义, 那么 $ f(t)\cdot p(x)=p(x+1)-p(x) $, 故 $ \Delta(E^n)=(E+1)^n-E^n $ 对任意哑元 $ E $ 和非负整数 $ n $ 成立.
只要按以上规则对哑元进行运算, 并正确解释其含义, 就能得到正确的结论.
另一种生成 $ P $ 上的线性变换的方式是, 定义 $ \lambda_{f,g}(x^n) $ 等于满足 $ \langle g(t)\left(f(t)\right)^k\mid p_n(x)\rangle=n!\delta_{nk} $ 的谢弗多项式列 $ p_n(x) $, 这种生成方式实际上包含了上一种方式, 因为 $ \lambda_{t,\frac{1}{g}} $ 就是将 $ x^n $ 映为阿佩尔多项式列 $ g(t)\cdot x^n $ 的线性变换.
线性变换的伴随将 $ L(P) $ 中的元素映为 $ L(P^*) $ 中的连续算子, 记所有连续算子组成的集合在加法, 数乘和复合下构成的 $ \mathbb{C} $ 代数为 $ CL(P^*) $, 则有代数同构
\[L(P)\cong CL(P^*)^{op},\]其中上标 $ op $ 代表反乘法下的反环.
一个重要的子集是哑算子 $ \lambda_{f,1} $, 它将 $ x^n $ 映为二项式型多项式列, 设二项式行列式列在哑复合下构成的非交换群为 $ \mathbb{B} $, 那么它同构于所有将 $ x^n $ 映为二项式型多项式列的线性变换在反复合下构成的群, 也由伴随同构于 $ \mathrm{Aut}(P^*) $ 在复合下构成的群, 由于每个将 $ x^n $ 映为二项式型多项式列的线性变换 $ \lambda_{f,1} $ 都对应一个存在复合逆的幂级数 $ f $, 所以 $ \mathbb{S} $ 在还同构于 $ (P^*,\circ)^\times $, 即有非交换群同构
\[\mathbb{B}\cong \left(\{\lambda:x^n\mapsto p_n(x)|p_n(x)\text{是二项式型多项式列}\},\circ\right)^{op}\cong\mathrm{Aut}(P^*)\cong(P^*,\circ)^\times.\]设 $ \mathbb{S} $ 是全体谢弗多项式列, 则有群同构
\[\mathbb{S}\cong\left(\{\lambda:x^n\mapsto p_n(x)|p_n(x)\text{是谢弗多项式列}\},\circ\right)^{op}\]因为 $ \lambda_{f,g} $ 是谢弗算子, 则 $ \lambda_{f,g}=\frac{1}{g(t)}\circ\lambda_f $ 说明有群同构
\[\mathbb{S}\cong\mathbb{A}\rtimes\mathbb{B}\cong(P^*,\cdot)^\times\rtimes(P^*,\circ)^\times.\]另一个重要的子集是哑移位 $ \theta $, 它将第 $ n $ 个二项式型多项式映为第 $ n+1 $ 个二项式型多项式列, 如果记 $ P^* $ 上所有满的导数算子组成的线性空间是 $ \mathrm{SDer}(P^*) $, 则有线性空间的同构
\[(\theta,+)\cong \left(\mathrm{SDer}(P^*),+\right).\]如果 $ \theta $ 是谢弗移位, 它将第 $ n $ 个谢弗多项式映为第 $ n+1 $ 个谢弗多项式列, 则有 $ \theta_{f,g}=\frac{1}{g(t)}\circ\theta_f\circ g(t) $, 这说明在 $ \mathrm{End}(P) $ 内, 所有谢弗移位组成的集合恰好就是 $ \mathbb{A} $ 在所有哑移位组成的集合上的共轭作用.
以上结论用图可以表示为:
参考文献
[1] Francesco Aldo Costabile, Modern Umbral Calculus: An Elementary Introduction with Applications to Linear Interpolation and Operator Approximation Theory, De Gruyter Studies in Mathematics, vol. 72, Walter de Gruyter, Berlin, Boston, 2019.
[2] Adriano M. Garsia, An exposé of the Mullin-Rota theory of polynomials of binomial type, Linear and Multilinear Algebra 1 (1973), no. 1, 47–65.
[3] Steven Roman, The Umbral Calculus, Pure and Applied Mathematics, vol. 111, Academic Press, New York, 1984.
[4] , Advanced Linear Algebra, 3rd ed., Graduate Texts in Mathematics, vol. 135, Springer, New York, 2008.