本文主要介绍椭圆积分理论基础, 主要目的是为椭圆函数论和椭圆曲线论提供背景, 因此省略椭圆积分理论的大部分计算性内容和严谨的分析学内容.
椭圆积分
椭圆周长
椭圆积分起源于求解椭圆周长问题.
不妨设椭圆方程为
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\]其中 $ b\ge a>0 $, 我们做换元 $ x=a\cos\theta $, $ y=b\sin \theta $, 其中 $\theta\in[0,2\pi)$. 于是椭圆周长可如下计算
\[\displaylines{ \int_0^{2\pi}\sqrt{\left(\frac{\mathrm{d}}{\mathrm{d}\theta}(a\cos\theta)\right)^2+\left(\frac{\mathrm{d}}{\mathrm{d}\theta}(b\sin\theta)\right)^2}\,\mathrm{d}\theta \\ =\int_0^{2\pi}\sqrt{a^2\sin^2\theta+b^2\cos^2\theta}\,\mathrm{d}\theta\\ =4b\int_0^{\frac{\pi}{2}}\sqrt{1-\frac{b^2-a^2}{b^2}\sin^2\theta}\,\mathrm{d}\theta, }\]设 $ k^2=\frac{b^2-a^2}{b^2} $, 则积分化为
\[4b\int_0^{\frac{\pi}{2}}\sqrt{1-k^2\sin^2\theta}\,\mathrm{d}\theta,\]由刘维尔的微分伽罗瓦理论可知该积分一般不存在初等表达式, 当 $k=0$ 时显然就是椭圆退化为圆的情况. 我们设
\[E(k,\varphi)=\int_0^{\varphi}\sqrt{1-k^2\sin^2\theta}\,\mathrm{d}\theta,\quad0\le k<1,\varphi\in\mathbb{R},\]称其为 不完全第二类椭圆积分 的勒让德形式, 当 $\varphi$ 取 $\frac{\pi}{2}$ 时记作
\[E(k)=\int_0^{\frac{\pi}{2}}\sqrt{1-k^2\sin^2\theta}\,\mathrm{d}\theta,\]称为 完全第二类椭圆积分 的勒让德形式, 于是椭圆周长即可表示为
\[4bE\left(\frac{b^2-a^2}{b^2}\right).\]顺带一提, 抛物线的弧长总是可以用初等函数表示, 双曲线的弧长也可以用略推广后的函数 $E(k,\varphi)$ 表示.
双纽线周长
椭圆曲线是到两点的距离和为定值的点的轨迹, 双曲线是到两点距离差为定值的点的轨迹, 抛物线是到一点和一条直线的距离相等的点的轨迹, 类似的, 可以找到一条曲线, 是到两点距离乘积为定值的点的轨迹, 称为卡西尼卵形线, 当该定值等于两点距离一半的平凡时, 显然两点的中点位于该曲线上, 这个特殊情况我们称为伯努利双纽线, 双纽线的一般方程为
\[(x^2+y^2)^2=2a^2(x^2-y^2),\]其中 $a$ 是正数, 我们现在来求双纽线的周长. 双纽线的参数方程为
\[\begin{cases} x = a\sqrt{2\cos 2\theta}\cos\theta \\ y = a\sqrt{2\cos 2\theta}\sin\theta \end{cases} , \quad \theta \in \left[-\frac{\pi}{4}, \frac{\pi}{4}\right] \cup \left[\frac{3}{4}\pi, \frac{5}{4}\pi\right],\]积分得
\[4\int_0^{\frac{\pi}{4}}\sqrt{\left(x'(\theta)\right)^2+\left(y'(\theta)\right)^2}\,\mathrm{d}\theta=4\int_0^{\frac{\pi}{4}}\frac{\sqrt{2}a}{\sqrt{\cos 2\theta}} \,\mathrm{d}\theta=4\int_0^{\frac{\pi}{4}}\frac{\sqrt{2}a}{\sqrt{1 - 2\sin^2\theta}} \,\mathrm{d}\theta ,\]做换元 $ 2\sin^2\theta = \sin^2\phi $, 上式化简为
\[4a \int_{0}^{\frac{\pi}{2}} \frac{\mathrm{d}\phi}{\sqrt{1 - \frac{1}{2}\sin^2\phi}},\]我们设
\[F(k,\varphi)= \int_{0}^{\varphi} \frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}},\]称其为 不完全第一类椭圆积分 的勒让德形式, 当 $\varphi$ 取 $\frac{\pi}{2}$ 时记作
\[K(k)=\int_0^{\frac{\pi}{2}}\frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}},\]称为 完全第一类椭圆积分 的勒让德形式, 于是双纽线周长即可表示为
\[4aK\left(\frac{1}{\sqrt{2}}\right).\]椭圆积分
椭圆积分一般指不能用初等函数表示的积分, 如果某些特殊情况积分可以由初等函数表示, 也有人称这些积分为伪椭圆积分. 如果将第一类和第二类椭圆积分的积分限舍去, 看做不定积分, 由以下的雅可比形式可得, 第一类椭圆积分和第二类椭圆积分自然是椭圆积分.
在第一类椭圆积分里做换元 $z=\sin\theta$ 得到
\[K(k)=\int_0^1\frac{\mathrm{d}z}{\sqrt{(1-z^2)(1-k^2z^2)}},\]称为第一类椭圆积分的雅可比形式.
在第二类椭圆积分里做换元 $z=\sin\theta$ 得到
\[E(k)=\int_0^1\sqrt{\frac{1-k^2z^2}{1-z^2}}\, \mathrm{d}z=\int_0^1\frac{1-k^2z^2}{\sqrt{(1-z^2)(1-k^2z^2)}}\, \mathrm{d}z,\]称为第二类椭圆积分的雅可比形式.
接下来定义第三类椭圆积分. 不完全第三类椭圆积分 的勒让德形式为
\[\Pi(h, \varphi, k) = \int_0^\varphi \frac{\mathrm{d}\theta}{(1 - h \sin^2 \theta)\sqrt{1 - k^2 \sin^2 \theta}},\]其中 $h$ 是取任意使得积分收敛的实数, 完全第三类椭圆积分 的勒让德形式为
\[\Pi(h, k) = \int_0^{\frac{\pi}{2}} \frac{\mathrm{d}\theta}{(1 - h \sin^2 \theta)\sqrt{1 - k^2 \sin^2 \theta}},\]对应的雅可比形式为
\[\int_0^{1}\frac{\mathrm{d}z}{(1-hz^2)\sqrt{(1-z^2)(1-k^2z^2)}},\]三类椭圆积分中, $ k $称为椭圆模, 第三类中$ h $ 称为椭圆特征.
最后叙述勒让德最知名的椭圆积分恒等式, 设 $ E’(k)=E(\sqrt{1-k^1}) $, $K’(k)=K(\sqrt{1-k^2})$.
应用: 算术几何平均数
设实数 $ a>b>0 $, 则
\[b<\sqrt{ab}<\frac{a+b}{2}<a,\]现取 $ a_0=a $, $ b_0=b $, $ a_1=\frac{a_0+b_0}{2} $, $ b_1=\sqrt{a_0b_0} $, $ a_{n+1}=\frac{a_n+b_n}{2} $, $ b_{n+1}=\sqrt{a_nb_n} $, 显然 $ b_n<b_{n+1}<a_{n+1}<a_n $, 于是数列 ${a_n}$ 和 ${b_n}$ 收敛到同一数, 记为 $ AGM(a,b) $, 称为两数的算术几何平均数.
我们设
\[M(a,b)=\int_0^{\frac{\pi}{2}}\frac{\mathrm{d}\theta}{\sqrt{a^2\cos^2\theta+ b^2\sin^2\theta}}.\]于是, 显然有
\[M(a,b)=M(a_1,b_1)=M(a_2,b_2)=\cdots=M(AGM(a,b),AGM(a,b)),\]又因
\[M(c,c)=\int_0^{\frac{\pi}{2}}\frac{\mathrm{d}\theta}{\sqrt{c^2\cos^2\theta+ c^2\sin^2\theta}}=\int_0^{\frac{\pi}{2}}\frac{\mathrm{d}\theta}{c\sqrt{\cos^2\theta+ \sin^2\theta}}=\frac{\pi}{2c},\]于是
\[M(a,b)=\frac{\pi}{2AGM(a,b)},\] \[AGM(a,b)=\frac{\pi}{2M(a,b)}.\]另一方面, 取 $ a=1 $, $b=\sqrt{1-k^1}$ 时,
\[M(1,\sqrt{1-k^2})=\int_0^{\frac{\pi}{2}}\frac{\mathrm{d}\theta}{\sqrt{\cos^2\theta+(1-k^2)\sin^2\theta}}=\int_0^{\frac{\pi}{2}}\frac{\mathrm{d}\theta}{\sqrt{1-k^2\sin^2\theta}}=K(k),\]我们令 $ k=i $, 则等式左边即为 $ M\left(1,\sqrt{2}\right) $, 右边为
\[K(i)=\int_0^1\frac{\mathrm{d}z}{\sqrt{(1-z^2)(1+z^2)}}=\int_0^1\frac{\mathrm{d}z}{\sqrt{(1-z^4)}},\]换元 $t=z^4$ 得
\[K(i)=\int_0^1 \frac{1}{4} t^{-\frac{3}{4}} (1-t)^{-\frac{1}{2}} dt = \frac{1}{4} B\left(\frac{1}{4}, \frac{1}{2}\right)=\frac{1}{4} \cdot \frac{\Gamma\left(\frac{1}{4}\right)\Gamma\left(\frac{1}{2}\right)}{\Gamma\left(\frac{3}{4}\right)}=\frac{\Gamma^2\left(\frac{1}{4}\right)}{4\sqrt{2\pi}},\]于是
\[AGM(1,\sqrt{2})^{-1}=\frac{\Gamma^2\left(\frac{1}{4}\right)}{(2\pi)^{\frac{3}{2}}},\]该数称为高斯常数, 常记为 $G$.
椭圆函数
椭圆积分起源于求椭圆周长, 在求圆的周长时, 不妨设半径为 $ 1 $, 得到的积分是
\[\int_0^a\sqrt{1-\left(\frac{\mathrm{d}}{\mathrm{d}x}\sqrt{1-x^2}\right)^2}\,\mathrm{d}x = \int_0^a \frac{\mathrm{d}x}{\sqrt{1 - x^2}}=\arcsin a,\]是反三角函数, 其反函数就是三角函数, 这启发我们可以研究椭圆积分的反函数, 阿贝尔, 雅可比和高斯分别意识到了这一点.
雅可比椭圆函数
考虑函数
\[u(\varphi)=F(k,\varphi)=\int_{0}^{\varphi} \frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}},\]其中 $0\le k<1$ 看做常数, 由于被积函数恒正, 则 $u$ 是从 $\mathbb{R}$ 到 $\mathbb{R}$ 的单调递增函数, 我们取 $u$ 的反函数, 记为
\[\varphi=\mathrm{am}(u),\]称为振幅函数, 因为它与单摆振幅有关. 令
\[\mathrm{sn}(u)=\sin(\mathrm{am}(u)),\] \[\mathrm{cn}(u)=\cos(\mathrm{am}(u)),\] \[\mathrm{dn}(u)=\frac{\mathrm{d}}{\mathrm{d}u}\mathrm{am}(u)=\sqrt{1-k^2\mathrm{su}^2(u)},\]它们统称为雅可比椭圆函数. 当 $k=0$ 时, 显然 $ u(\varphi)=\varphi $, 于是 $ \mathrm{sn}(u)=\sin u $, $ \mathrm{cn}(u)=\cos u $, 因此三角函数也称为圆函数. 另外还有一种特殊情况,
\[\mathrm{sl}(u)=\frac{1}{\sqrt{2}}\mathrm{sn}\left(\sqrt{2}u,\frac{1}{\sqrt{2}}\right),\] \[\mathrm{cl}(u)=\frac{1}{\sqrt{2}}\mathrm{cn}\left(\sqrt{2}u,\frac{1}{\sqrt{2}}\right),\]称为双纽函数, 它们由高斯引进, 与双纽线和算术几何平均值有密切联系.
雅可比椭圆函数的性质
接下来看看雅可比椭圆函数有哪些性质, 显然的, 由三角函数的性质即得
\[\displaylines{ \int_0^{\varphi+\pi} \frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}} =\int_0^\varphi\frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}}+\int_\varphi^{\varphi+\pi} \frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}}\\ =\int_0^\varphi\frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}}+\int_0^{\pi}\frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}}\\ =\int_0^\varphi \frac{\mathrm{d}\theta}{\sqrt{1 - k^2\sin^2\theta}}+2K(k) }\]其中 $ K(k) $是完全第一类椭圆积分, 于是$ \mathrm{am}(u+2K(k))=\mathrm{am}(u)+\pi $, 因此
\[\mathrm{sn}(u+2K(k))=-\mathrm{sn}(u),\quad\mathrm{sn}(u+4K(k))=\mathrm{sn}(u),\] \[\mathrm{cn}(u+2K(k))=-\mathrm{cn}(u),\quad\mathrm{cn}(u+4K(k))=\mathrm{cn}(u),\] \[\mathrm{dn}(u+2K(k))=\mathrm{dn}(u),\]以后我们简记 $ K(k) $为$ K $, 简单计算有
\[\mathrm{sn}(0)=0,\quad\mathrm{sn}(K)=1,\] \[\mathrm{cn}(0)=1,\quad\mathrm{cn}(K)=0,\] \[\mathrm{sn}(0)=1,\quad\mathrm{sn}(K)=\sqrt{1-k^2},\]可以画出它们的图像, 体现了它们与三角函数的相似性.
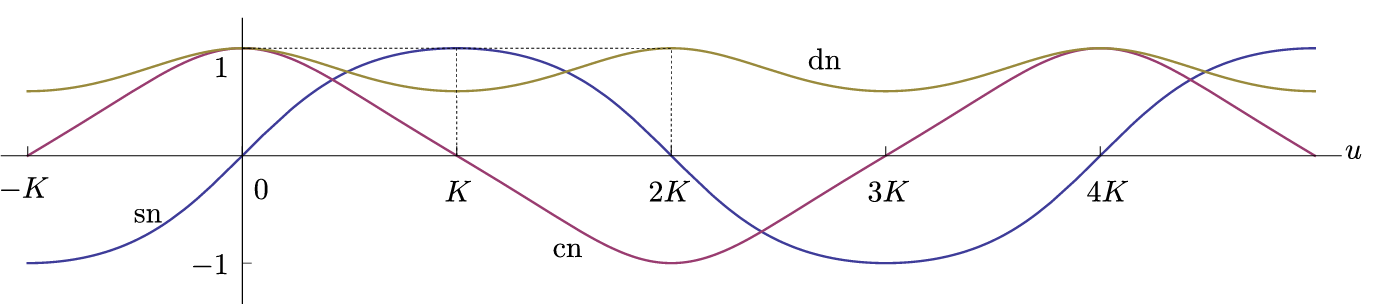
在我们的定义中, $k$ 不能取到 $ 1 $, 但当 $k$ 趋于 $1$ 时, 雅可比椭圆函数的极限是有意义的, 事实上, 可以证明
\[\mathrm{sn}(u)\to\tanh u=\frac{\sinh u}{\cosh u},\quad\mathrm{cn(u),\mathrm{dn}(n)\to\frac{1}{\cosh u}}\]为双曲函数.
雅可比椭圆函数有以下求导性质:
\[\frac{\mathrm{d} }{\mathrm{d} u}\mathrm{sn}(u) = \mathrm{cn}(u) \mathrm{dn}(u),\] \[\frac{\mathrm{d} }{\mathrm{d} u}\mathrm{cn}(u) = -\mathrm{sn}(u) \mathrm{dn}(u),\] \[\frac{\mathrm{d} }{\mathrm{d} u}\mathrm{dn}(u) = -k^2 \mathrm{sn}(u) \mathrm{cn}(u).\]雅可比椭圆函数有以下加法公式:
\[\mathrm{sn}(u+v) = \frac{\mathrm{sn}(u)\mathrm{cn}(v)\mathrm{dn}(v) + \mathrm{cn}(u)\mathrm{sn}(v)\mathrm{dn}(u)}{1 - k^2 \mathrm{sn}^2(u)\mathrm{sn}^2(v)},\] \[\mathrm{cn}(u+v) = \frac{\mathrm{cn}(u)\mathrm{cn}(v) - \mathrm{sn}(u)\mathrm{sn}(v)\mathrm{dn}(u)\mathrm{dn}(v)}{1 - k^2 \mathrm{sn}^2(u)\mathrm{sn}^2(v)},\] \[\mathrm{dn}(u+v) = \frac{\mathrm{dn}(u)\mathrm{dn}(v) - k^2 \mathrm{sn}(u)\mathrm{sn}(v)\mathrm{cn}(u)\mathrm{cn}(v)}{1 - k^2 \mathrm{sn}^2(u)\mathrm{sn}^2(v)}.\]雅可比椭圆函数推广到复数
接下来的工作是将雅可比椭圆函数的定义域推广到复数.
我们要求 $ \mathrm{sn}(iu) $, 就是要求 $iu = \int_{0}^{x} \frac{\mathrm{d} t}{\sqrt{(1-t^2)(1-k^2t^2)}}$ 中的 $ x $, 令 $ t=iz $, 得
\[iu = \int_{0}^{-ix} \frac{i \mathrm{d} z}{\sqrt{(1 + z^2)(1 + k^2z^2)}},\] \[u = \int_{0}^{-ix} \frac{\mathrm{d} z}{\sqrt{(1 + z^2)(1 + k^2z^2)}},\]再换元 $z = \frac{\varphi}{\sqrt{1-\varphi^2}}$ 得
\[u = \int_{0}^{\varphi_0} \frac{\mathrm{d} \varphi}{\sqrt{(1-\varphi^2)(1-k'^2\varphi^2)} },\quad k'=\sqrt{1-k^2}\]其中
\[-ix = \frac{\varphi_0}{\sqrt{1-\varphi_0^2}},\]对比定义可知 $ \varphi_0=\mathrm{sn}(u,k’) $, 于是 $ \sqrt{1-\varphi_0^2}=\mathrm{cn}(u,k’) $, 故
\[\mathrm{sn}(iu,k) = x = i \frac{\mathrm{sn}(u, k')}{\mathrm{cn}(u, k')},\]再根据加法公式即可推广到整个复平面上, 另外两个函数也可类似处理.
设 $ K’=K(k’)=K\left(\sqrt{1-k^2}\right) $, 由此得到虚循环性质
\[\mathrm{sn}(u+2K'i) = i \frac{\mathrm{sn}(-i(u+2K'i), k')}{\mathrm{cn}(-i(u+2K'i), k')}=i \frac{\mathrm{sn}(-iu+2K', k')}{\mathrm{cn}(-iu+2K', k')}=i \frac{-\mathrm{sn}(-iu, k')}{-\mathrm{cn}(-iu, k')}=\mathrm{sn}(u),\]即雅可比椭圆函数是复平面上以 $4K$ 和 $2K’i$ 为周期的双周期亚纯函数, 周期为长方形格点, 对于 $ \mathrm{cn}(u) $, 可计算得它是以 $4K$ 和 $2K+2K’i$ 为周期的双周期函数, 周期为菱形格点, $\mathrm{dn}(u)$ 是以 $2K$ 和 $4K’i$ 为周期的双周期函数, 周期也为长方形格点.
雅可比椭圆函数在复平面上关于实轴对称, 而复平面上沿实轴对称的格点只有长方形和菱形两种, 之后会看到一些未必对称的椭圆函数.
雅可比theta函数
现代的雅可比 $\theta$ 函数一般定义为
\[\theta(z,\tau)=\sum_{n=-\infty}^\infty e^{\pi in^2\tau}e^{2\pi inz}=\sum_{n=-\infty}^\infty q^{n^2}\eta^n,\]其中 $ z\in\mathbb{C} $, $\tau\in \mathbb{H}$ 为上半平面, 习惯做代换 $ q=e^{\pi i\tau} $, $ \eta=e^{2\pi iz} $, 显然 $q\in D$ 为单位开圆盘, $\eta\in \mathbb{C}^\times=\mathbb{C}-{0}$.
雅可比的原始定义中包含四个函数:
\[\theta_1(z, \tau) = -i e^{i \frac{\pi \tau}{4} + i \pi z} \theta\left(z + \frac{1}{2} + \frac{\tau}{2}, \tau\right) = \sum_{n=-\infty}^{\infty} (-1)^{n-\frac{1}{2}} e^{i \pi \left(n+\frac{1}{2}\right)^2 \tau }e^{\pi i (2n+1) z},\] \[\theta_2(z, \tau) = e^{i \frac{\pi \tau}{4} + i \pi z} \theta\left(z + \frac{\tau}{2}, \tau\right) = \sum_{n=-\infty}^{\infty} e^{i \pi \left(n+\frac{1}{2}\right)^2 \tau }e^{\pi i (2n+1) z},\] \[\theta_3(z, \tau) = \theta(z,\tau)=\sum_{n=-\infty}^\infty e^{\pi in^2\tau}e^{2\pi inz},\] \[\theta_4(z, \tau) = \theta\left(z + \frac{1}{2}, \tau\right) = \sum_{n=-\infty}^{\infty} (-1)^n e^{i \pi n^2 \tau + 2 \pi i n z},\]由定义立刻得到 $\theta$ 函数的拟周期性
\[\theta(z,\tau)=\theta(z+1,\tau),\] \[\theta(z+\tau,\tau)=e^{-\pi i(\tau+2z)}\theta(z,\tau).\]当 $z=0$ 时, 也简记 $ \theta(0,\tau)=\theta(\tau) $, 而固定 $ \tau $, $\theta(z,\tau)$ 关于 $z$ 是 $\mathbb{C}$ 上的整函数, 雅可比证明了, 设 $ z=\frac{u}{2K} $, 则有
\[\mathrm{sn}(u) = \frac{\theta_3(\tau)}{\theta_2(\tau)}\frac{\theta_1(z, \tau)}{\theta_4(z, \tau)},\] \[\mathrm{cn}(u) = \frac{\theta_4(0)}{\theta_2(0)} \frac{\theta_2(z, \tau)}{\theta_4(z, \tau)},\] \[\mathrm{dn}(u) = \frac{\theta_4(0)}{\theta_3(0} \frac{\theta_3(z, \tau)}{\theta_4(z, \tau)}.\]雅可比 $\theta$ 函数与模形式有很深的联系, 事实上, $\theta_3^4(\tau)$ 就是权为 $ 2 $, 级为 $\Gamma(2)$ 的模形式, 而且 $\theta_2^4(\tau)$ 和 $\theta_4^4(\tau)$ 是权为 $ 2 $, 级为 $\Gamma(2)$ 的模形式空间里的一组基, 例如, $\theta_3^4(\tau)$ 可以由以下雅可比恒等式表示:
\[\theta_3^4(\tau) = \theta_2^4(\tau) + \theta_4^4(\tau),\]这给出四次费马曲线的参数化.
它们还与其他模形式有密切关系, 例如模 $\lambda$ 函数
\[\lambda(\tau)=\frac{\theta_2^4(\tau)}{\theta_3^4(\tau)},\]艾森斯坦因级数
\[E_4(\tau) = \frac{1}{2}(\theta_2^8(\tau) + \theta_3^8(\tau) + \theta_4^8(\tau)),\]模判别式
\[\Delta(\tau) = \frac{1}{256} \theta_2^8(\tau) \theta_3^8(\tau) \theta_4^8(\tau),\]模不变量
\[j(\tau) = 32 \frac{\left(\theta_2^8(\tau) + \theta_3^8(\tau) + \theta_4^8(\tau)\right)^3}{\theta_2^8(\tau) \theta_3^8(\tau) \theta_4^8(\tau)}.\]魏尔斯特拉斯椭圆函数
按雅可比椭圆函数的双周期性的思路推广, 得到的就是魏尔斯特拉斯椭圆函数.
首先设 $\omega_1$ 和 $\omega_2$ 是两个实线性无关的复数, 这等价于它们的比不是实数, 也等价于它们构成 $\mathbb{C}$ 作为实向量空间的一组基, 设函数 $f$ 是满足 $ f(z+\omega_1)=f(z) $, $f(z+\omega_2)$ 的函数, 则称它是一个双周期函数.
设
\[\Lambda=\{a\omega_1+b\omega_2\mid a,b\in\mathbb{Z}\},\]称为复平面上的一个格点, 以 $\omega_1$ 和 $\omega_2$ 为周期的双周期函数也说是以 $\Lambda$ 为周期的双周期函数.
以下定理完全分类了复环面.
以后我们记商映射 $\pi\colon \mathbb{C}\to\mathbb{C}/\Lambda$ 将 $z$ 映为等价类 $ [z] $.
其收敛性不在此证明, 常省略格点, 简写为 $\wp(z)$. 首先注意到它在原点处有一个二重极点, 由格点性质即得双周期性, 并且是一个偶函数, 因此可以将它同时视为复数域上的双周期亚纯函数或复环面上的亚纯函数. 对它逐项求导即得
\[\wp'(z) = -2 \sum_{w \in \Lambda} \frac{1}{(z-w)^3},\]可以证明, 任何椭圆函数都可以由魏尔斯特拉斯函数及其导数加减乘除组合得到, 也就是说, 设椭圆函数域为 $ \mathscr{E} $, 则 $\mathscr{E}\cong \mathbb{C}(\wp,\wp’)$.
魏尔斯特拉斯证明了关系式
\[(\wp'(z))^2 = 4\wp(z)^3 - g_2\wp(z) - g_3,\]其中 $ g_2 = 60 \sum_{w \in \Lambda \setminus \{0\}} \frac{1}{w^4} $, $g_3 = 140 \sum_{w \in \Lambda \setminus \{0\}} \frac{1}{w^6}$ 是艾森斯坦因级数, 注意到该关系式与椭圆曲线方程类似, 我们做映射
\[\displaylines{ \mathbb{C}/\Lambda\to \mathbb{CP}^2\\ \quad\quad\quad\quad z\mapsto \begin{cases} (\wp(z):\wp'(z):1),\quad z\neq [0];\\ (0:1:0),\quad z=[0]. \end{cases} }\]是一个嵌入映射, 将复环面映为复射影平面内一条曲线, 即椭圆曲线.
椭圆曲线
椭圆曲线源于椭圆积分中的代数方程 $ y^2=p(x) $, 其中 $ p $是三次或四次多项式, 我们可以对$ p $ 的系数和定义域限制在某个域 $ k $内, 例如$ \mathbb{C} $, $ \mathbb{R} $, $ \mathbb{Q} $, 有限域 $\mathbb{F}_p$ 或 $p$ 进域 $\mathbb{Q}_p$ 等, 我们这里仅分为复数情况和有理数情况, 并在最后一节讨论推广.
复椭圆曲线
复数域上的椭圆曲线有以下几种等价定义, 本节主要说明他们的等价性.
- 1, 亏格为 $1$ 的紧黎曼曲面;
- 2, 一维复环面 $ \mathbb{C}/\Lambda $;
- 3, 非退化魏尔斯特拉方程定义的射影曲线;
- 4, 亏格为 $1$ 的非奇异射影曲线;
- 5, 一维非奇异射影代数群.
首先需要详细说明这些定义.
1, 黎曼曲面即连通的一维复流形, 其亏格定义为其第一个德拉姆上同调群的维数的一半 $\frac{1}{2}\dim_\mathbb{R} H^1_{dR}(M)=g$. 黎曼曲面之间的态射为全纯映射.
2, 复环面先前已定义过了, 它是亏格为 $1$ 的紧黎曼曲面, 态射为全纯映射.
3, 魏尔斯特拉斯方程为
\[y^2=x^3+Ax+B,\]非退化指判别式 $ \Delta=4A^3+27B^2\neq 0 $, 它给出 $\mathbb{C}^2$ 中的一条曲线, 将它齐次化
\[y^2z=x^3+Axz^2+Bz^3,\]将曲线上的点 $(x,y)$ 嵌入 $ \mathbb{CP}^2 $, 按齐次坐标表示为 $ (x:y:1) $, 这相当于在曲线上添加一个无穷远点 $ \infty=(0:1:0) $, 成为 $\mathbb{CP}^2$ 中的一条曲线, 它与 $\mathbb{CP}^2$ 中的无穷远线相交于 $\infty$ 处. 曲线间态射为保持无穷远点的正则映射.
4, 亏格为 $1$ 的非奇异射影曲线即满足一些条件的一维概形, 态射为概形同态.
5, 即带群结构的一维非奇异射影簇, 态射为代数群同态.
显然2是1的特殊情况, 而由阿贝尔-雅可比定理即可得到1与2的等价, 2中的加法群结构也可以诱导到1上. 由魏尔斯特拉斯函数参数化可由2得到3, 而3是4的特殊情况, 由黎曼存在定理可由1得到4, 再使用解析化可由4得到1. 由黎曼-罗赫定理也可由4得到3. 5无非是带群结构的4, 而1, 2, 3, 4的群结构均可由2诱导.
另外需要注意基点的问题, 1的基点可任意选取, 2的基点选为原点 $0$ 的等价类 $ [0] $, 3的基点选为无穷远点, 4的基点可任意选取, 5的基点选为群单位元 $ e $, 各定义间的转换应保持基点.
我们将以上几种等价定义的东西统一称为复数域上的椭圆曲线, 椭圆曲线范畴记为 $ \mathsf{Ell}_\mathbb{C} $, 其中态射均保持基点.
椭圆曲线有理点
一条由魏尔斯特拉斯标准型定义的椭圆曲线, 如果系数均为有理数, 则称该椭圆曲线定义在有理数域上, 再限制 $x$ 和 $ y $只取有理数或无穷远点, 则这些点称为椭圆曲线$ E $ 的有理点 $ E(\mathbb{Q}) $, 这些点之间的加法与复数域情况相同, 由解析几何可知在该加法下 $E(\mathbb{Q})$ 是一个阿贝尔群.
推广
椭圆曲线的推广有两个方向, 其一是从复数域推广到其他域, 其二是从一维推广到高维, 前者得到椭圆曲线概形, 后者则推出阿贝尔簇.
任意域 $k$ 上的椭圆曲线定义为亏格为 $1$ 的非奇异射影代数曲线.
对任意正整数 $ n $, 设 $\Lambda$ 为 $2n$ 维格点, 即 $\mathbb{C}^n$ 中的格点, 商空间 $\mathbb{C}^n/\Lambda$ 称为 $n$ 维复环面, 复环面完全确定了紧连通复李群.
$ 1 $维的时候, 先前已经说明$ 1 $ 维复环面一定能嵌入 $ \mathbb{CP}^2 $, 说明一维阿贝尔簇即为椭圆曲线.